Lexikon der Physik: Mathematische Physik - Erfolge und Mißerfolge
Mathematische Physik – Erfolge und Mißerfolge
Walter Thirring, Wien
Vielfach gewinnt man den Eindruck, Aufgabe der mathematischen Physik sei es, die Physik durch veredelnde Abstraktionen von allen irdischen Schlacken zu reinigen und sie so in eine Sphäre zu entrücken, in die naive Vorstellungsgabe und gesunder Menschenverstand nicht folgen können. Die Probleme scheinen jedoch anderswo zu liegen: Die grundlegenden Naturgesetze sind in den weitesten Bereichen bekannt, das Unbekannte ist auf die Physik des ganz Kleinen und des ganz Großen zusammengeschmolzen. Aber die menschliche Rechenkunst ist nur in den einfachsten Fällen imstande, tatsächlich aus den Gesetzen Resultate mathematisch abzuleiten. Meistens muß man, von der Intuition geführt oder verführt, zu unkontrollierbaren Näherungen Zuflucht nehmen. So zerbröckelt die logische Einheit, und die Wissenschaft wird zur Kunde unzähliger Spezialgebiete mit eigener Sprache und Folklore. Nun hat sich die Mathematik in den letzten hundert Jahren doch soweit entwickelt, daß sie uns Fragen beantwortet, denen die Intuition zunächst hilflos gegenübersteht, da sie in dieser Richtung nie geschult wurde. So gewährt die mathematische Physik vielfach tiefere Einsichten, welche durch einfache Argumente nicht zu gewinnen sind, und kann so manche Lücke füllen. Dies soll an drei der härtesten Nüsse, die in den sechziger und siebziger Jahren in der mathematischen Physik geknackt wurden, illustriert werden. Sie machen auch klar, daß es sich keineswegs um Epsilontik oder Details handelt, sondern vielmehr um grundlegende qualitative Züge.
1. Der KAM-Satz
Die meisten Beispiele, die man in Büchern über klassische Mechanik findet, sind sogenannte integrable Systeme. Hat das System n Freiheitsgrade, so haben sie n konstante Wirkungsvariable und n Winkelvariable. Ein Prototyp davon sind etwa n harmonische Oszillatoren mit der Hamilton-Funktion
![](javascript:ShowPic("/lexika/images/physik/fff7495.jpg", "633", "80");)
.
Hier gibt es die n Konstanten 
, und die Bahn erfüllt daher nicht die ganze (2n – 1)-dimensionale Energieschale, sondern höchstens einen n-dimensionalen Torus. Die Klasse der integrablen Systeme ist etwas allgemeiner, für sie können die Omegas von den Wirkungsvariablen abhängen. Ein integrables System verhält sich daher nicht ergodisch und strebt somit auch keinem Gleichgewicht zu. Durch fast hundert Jahre hindurch war nun die Ansicht verbreitet, daß es sich bei (1) um einen entarteten Fall handele und daß durch eine kleine Störung (›Kohlestäubchen‹) die Konstanten außer H zerstört würden und sich ein Gleichgewicht einstellte. Sogar E. Fermi glaubte noch, dies mathematisch beweisen zu können. Man verdankt den Arbeiten von Kolmogorow, Arnold und Moser die Einsicht, daß dem nicht so ist, daß durch eine kleine Störung die meisten Tori nur deformiert werden, die Bahn im allgemeinen daher wieder auf eine n-dimensionale Fläche gebannt bleibt. Da es sich dabei um eine der grundlegenden Fragen des Vielkörperproblems handelt, soll kurz untersucht werden, wieso hier Fermis sonst so brillante Intuition überfordert war.
Bei periodischen Bewegungen wird der Effekt einer Störung zeitlich gemittelt und bleibt daher klein, es sei denn, er wird durch Resonanzeffekte aufgeschaukelt. Dies ist schon im einfachsten Fall ersichtlich: Addiert man etwa zu (1) mit n = 2 eine Störung 
, so werden die neuen
![](javascript:ShowPic("/lexika/images/physik/fff7498.jpg", "669", "56");)
Dies läßt sich nach 
entwickeln, solange 
. Die Störung hat also kleinen Einfluß, außer wenn die Frequenzen fast entartet sind. Der KAM-Satz verallgemeinert dies zur Aussage, daß die Störung bei rationaler Abhängigkeit der Frequenzen die Eigenschaften des Systems verändern kann; sind die 
aber genügend rational unabhängig, ist man also genügend weit weg von den Resonanzen, so verformt sie nur etwas die Tori, welche die Bahn umrankt. Aber was heißt genügend rational unabhängig? Die rationalen Zahlen liegen ja auf der Zahlengeraden dicht und durch ganzzahlige Kombinationen zweier rational unabhängiger Frequenzen läßt sich jede Frequenz beliebig genau approximieren. Es ist also alles mit fast allem irgendwie rational verwandt und schwingt daher mit. Aber so wie die entfernten Obertöne, obgleich dissonant, die Musik nicht stören, da sie nur ganz schwach angeregt werden, so sind auch hier jene 
, für die
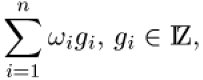
nur klein wird, wenn die gi sehr groß werden, weniger wirksam. Das genaue Kriterium ist nämlich, daß, falls für all n-Tupel ganzer Zahlen (gi)
![](javascript:ShowPic("/lexika/images/physik/fff7504.jpg", "639", "80");)
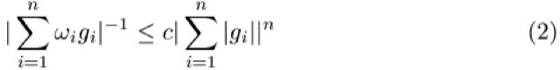
gilt, die invarianten Tori durch Störungen, deren Stärke unter einer gewissen fallenden Funktion von c liegt, nur etwas verformt werden. Dabei müssen die ω von den Winkelvariablen abhängen, und nur die Tori, die so im Phasenraum liegen, daß (2) verletzt ist, werden daher zerstört. Dies ist nun an allen rationalen Punkten des n-dimensionalen Raumes der ω der Fall, und man könnte voreilig schließen, daß dann nichts Unzerstörtes überbleibt. Tatsächlich ist das Maß der ω, die (2) mit genügend kleinem c erfüllen, in jeder Kugel fast das ganze Maß der Kugel. Man hat hier das von den Cantor-Mengen (Cantorus) her bekannte Paradoxon einer nirgends dichten Menge – ihr Komplement ist offen und enthält die rationalen Punkte –, deren Maß aber fast das ganze Maß ausschöpft. Das einfachste Beispiel dafür erhält man, indem man die rationalen Zahlen irgendwie durchnumeriert, etwa rn, 
, und durch immer kleinere offene Intervalle einschließt:
ist offenbar offen und dicht, hat aber ein Maß 
. Ganz analog ist die Menge der ω, die (2) verletzen, gebaut. Sie enthält die rationalen Punkte, hat aber kleines Maß, da für Resonanzen weiterer Verwandtschaft ( 
groß) 
groß werden darf, also nur kleine Frequenzgebiete ausgeschlossen werden. Es ist klar, daß die Physiker der zwanziger Jahre auf diese Unterscheidung des topologischen Begriffs einer nirgends dichten Menge und des maßtheoretischen Begriffs einer Menge kleinen Maßes nicht vorbereitet waren. Da das Maß 
als Wahrscheinlichkeitsmaß im Phasenraum zu interpretieren ist, ist der maßtheoretische Begriff der physikalisch relevante. Meistens wird man sich im Phasenraum an einem solchen Punkt befinden, für den der Torus durch ihn nur verformt wird. Da aber Tori in unmittelbarer Nähe zerstört werden, ist die Situation so kompliziert, daß eine Lösung dieser so grundlegenden Frage durch ein einfaches Argument zum Scheitern verurteilt ist. Leider werden daher die Abschätzungen für die Konstante c so roh, daß man für eine größere Zahl von Freiheitsgraden n nur für lächerlich kleine Störungen ein Resultat bekommt. Ob dies nur an der Beweismethode liegt und der Satz für das echte Vielkörperproblem Relevanz hat, ist eine noch offene Frage.
2. Gravitationskollaps und Singularitätensätze
Vor Beginn des Zweiten Weltkrieges hat Robert Oppenheimer mit verschiedenen Mitarbeitern Lösungen zu den Einstein-Gleichungen gefunden, die den Zusammenbruch eines Sternes beschreiben. Er zieht sich in endlicher Eigenzeit auf einen Punkt zusammen, und es verbleibt nur eine Singularität in der Metrik. Dieses Geschehen ist vielleicht nicht so verwunderlich, da in der Lösung nur eine rein radiale Bewegung studiert wird: Wenn alles scharf auf den Mittelpunkt zielt, muß es ja dort zur Katastrophe kommen. Spezifisch von der Einsteinschen Theorie geht nur ein, daß Druck ebenfalls Gravitation erzeugt und nicht hilft, den Kollaps aufzuhalten. Man könnte jedoch vermuten, daß sich bei Bewegung mit Drehimpuls das Schicksal wendet, und vielfach wurde behauptet, daß es sich hier nur um eine Pathologie einer Lösung mit zu großer Symmetrie handele. So glaubten Lifschitz und Mitarbeiter zeigen zu können, daß im allgemeinen keine Singularität entsteht. Das Interesse an dem Problem liegt auf der Hand, geht es doch um folgendes: bildet sich nur unter so speziellen Umständen ein Schwarzes Loch, daß es praktisch nie dazu kommt, oder geschieht dies für die meisten Anfangsbedingungen, so daß es im Weltall von Schwarzen Löchern nur so wimmeln sollte? Die Frage wurde zugunsten letzterer Alternative (in abgeschwächter Form) von R. Penrose und anderen Forschern aus der Schule von D. Sciama beantwortet. Zu diesem Schluß kommt man im einfachsten Fall durch Kombination eines simplen physikalischen Tatbestandes mit einer sehr plausibel klingenden geometrischen Behauptung. Da sie aber eine globale Aussage ist, birgt sie den nichttrivialen Teil und erklärt, warum sich dabei durch das übliche Herumrechnen mit der Einsteinschen Gleichung nichts entscheiden läßt.
Zunächst benützt man die einfach zu beweisende Tatsache, daß Bahnen frei fallender Teilchen, wenn sie einmal konvergieren, durch die Gravitation in dieser Tendenz höchstens bestärkt werden. Dies drückt nur die anziehende Natur der Schwerkraft aus und gilt schon nichtrelativistisch, sofern alle Massen positiv sind. Letzteres wird in der Einsteinschen Theorie durch die Forderung ersetzt, daß Energiedichte + Druck positiv sein müssen. Man kann dann leicht sehen, daß sich konvergierende Weltlinien nach endlicher Zeit überkreuzen müssen. Dies ist an sich kein Malheur und kann ohne weiteres auch im flachen Raum geschehen, wo die Weltlinien frei fallender Teilchen Geraden sind. Hier setzt nun das geometrische Argument ein, welches benützt, daß die Weltlinien frei fallender Teilchen geodätische Linien sind. Von einer raumartigen Anfangsfläche ist zu jedem Punkt die Bahn mit längster Eigenzeit eine geodätische Linie, welche im Sinne der Lorentz-Metrik senkrecht auf der Fläche steht. Überkreuzen sich aber zwei benachbarte geodätische Linien, können sie nicht Bahnen längster Eigenzeit sein, denn durch Abrunden der Ecke kann man eine Bahn konstruieren, auf der längere Zeit zur Fläche verstreicht. Hier braut sich ein Widerspruch zusammen, denn man wird erwarten, daß es von jedem Punkt eine längste Linie zur Anfangsfläche gibt. Dies läßt sich auch zeigen, sofern jede geodätische Linie durch den Punkt die Anfangsfläche schneidet. Dies ist natürlich zu verlangen, denn schon in der euklidischen Ebene (siehe Abb. 1 ) gibt es vom Punkt (0, 1) keine kürzeste Gerade zur positiven x-Achse 
.
Ferner kann es auch geschehen, daß sich zwar geodätische Linien kreuzen, durch jeden Punkt aber auch ungekreuzte gehen, dann sind eben letztere die extremalen Linien. Dies sieht man wieder in der Ebene, wenn man nach der kürzesten Linie von einem Punkt P zu einer gekrümmten Anfangsfläche fragt. Sie ist die Gerade senkrecht zur Fläche, welche sich nicht mit ihren Nachbarn kreuzt (siehe Abb. 2 ).
Hat man nun eine Anfangsfläche, so daß sie jede zeitartige geodätische Linie durch einen Punkt schneidet, und konvergieren auf der Anfangsfläche alle senkrechten geodätischen Linien so, daß sie sich vor dem Punkt mit ihren Nachbarn kreuzen, dann gerät man in einen Widerspruch. Es müßte von dem Punkt eine Linie längster Eigenzeit zur Fläche geben, sie müßte eine ungekreuzte geodätische Linie senkrecht zur Fläche sein, solche gibt es aber nicht. Die Schlußfolgerung ist, daß sich der Raum nicht bis zum Punkt fortsetzen läßt. Man sieht hier sofort die Schwäche der Aussage, die durch die geometrische Natur des Arguments entsteht. Es wird nicht gesagt, was physikalisch eigentlich geschieht, sondern man erfährt nur, daß Beobachter nach endlicher Eigenzeit ans Ende der Welt kommen und dann nicht recht wissen, was sie tun sollen, da die Naturgesetze nicht weiter spezifiziert sind. Vermutlich macht sich das Ende der Welt durch immer größer werdende Gezeitenkräfte bemerkbar und wird von niemandem lebend erreicht.
3. Stabilität der Materie
In der Thermodynamik wird postuliert, daß die Energie eine extensive Größe ist, die Energie pro Teilchen für ein großes System einem Grenzwert zustrebt. Da gewöhnliche Materie aus Elektronen und Atomkernen besteht, und diese einer Schrödingergleichung
![](javascript:ShowPic("/lexika/images/physik/fff7514.jpg", "567", "33");)
genügen, wäre
![](javascript:ShowPic("/lexika/images/physik/fff7516.jpg", "567", "33");)
, mit A einer Konstanten von der Ordnung der Rydberg-Energie, zu zeigen. Es ist bemerkenswert, daß die Gleichung (3) durch Jahrzehnte etwa in der Festkörperphysik verwendet wurde, wobei man die fundamentale Ungleichung (5) immer vorausgesetzt, aber nie bewiesen hat. Erst 1965 ist es Dyson und Lenard gelungen, (5) zu beweisen. Diese Ungleichung versichert uns, daß der Zustand der Materie um uns nahe dem tatsächlichen Grundzustand ist, und letzterer nicht etwa unheimlich hohe Dichte und Bindungsenergie hat. So plausibel dies klingen mag, so schwer ist es, (5) zu beweisen. Zunächst hat man den trivialen Umstand, daß in (4) eine Doppelsumme mit ˜ N2 Termen steht, und wenn etwas ˜ N herauskommen soll, so muß sich sehr viel kompensieren. Haben alle Terme dasselbe Vorzeichen, wie es etwa beim Gravitationspotential der Fall ist, besteht keine Chance für Stabilität. Aber auch für Coulomb-Kräfte gilt (5) nicht allgemein, wie folgendes naive Argument zeigt. Ist das System in einem Volumen ˜ R3, so ist wegen der Unschärferelation die kinetische Energie (ohne Fermi-Dirac-Statistik) 
. Für die potentielle Energie nehmen wir an, daß sich die Ladungen abwechselnd positiv und negativ verteilen. Dann hat jede Ladung umgekehrt geladene Nachbarn, und das Feld der Ladungen weiter weg wird abgeschirmt. Die potentielle Energie wird dann -e2N / (Abstand zum nächsten Nachbarn) ˜ -e2N4 / 3 / R. Das Minimum der Summe beider Energien ergibt sich für R ˜ N-1 / 3 zu EN ˜ -N5 / 3. Nur wenn durch Fermi-Dirac-Statistik die kinetische Energie pro Teilchen nicht mit R-2, sondern mit (R / N1 / 3)-2 ansteigt, ergibt sich ein Minimum für R ˜ N1 / 3, das wie EN ˜ -N geht. Dieses Argument ist natürlich sehr roh und nicht schlüssig, man sieht aber folgendes:
l. Bei Instabilität fällt R mit wachsendem N, die Dichte wird immer größer, um die Singularität des Coulomb-Potentials besser auszunützen. Es ist also nicht die lange Reichweite des 1 / r-Potentials, welche die Stabilität bedroht, und daher ist sie für ein Yukawa-Potential und für Kernmaterie genau so schwer zu beweisen.
2. Entfernt man die 1 / r-Singularität durch einen Formfaktor bei 10-13 cm, so erhält man zwar Stabilität, aber sicher nicht die richtige Erklärung dafür. Dies würde ja in (5) 
geben, man sucht aber 
.
3. Aus der Erfahrung, die man von Molekülberechnungen gewinnt, läßt sich nicht auf die Stabilität der Materie schließen. Genauer kann man ja doch nur Moleküle mit ein oder zwei Elektronen berechnen, und hier kommt die Fermi-Dirac-Statistik noch nicht ins Spiel. Man würde so also auch auf Stabilität für Elektronen mit Bose-Einstein-Statistik schließen, was aber falsch ist.
Dyson und Lenard haben einen heroischen Frontalangriff auf dieses schwierige Problem unternommen. In einer langen Analyse haben sie aus den durch die Fermi-Dirac-Statistik erzwungenen Nullstellen von 
genügend kinetische Energie herausgewirtschaftet, um (5) zu zeigen. Der Preis war hoch, A war von der Ordnung 1014 Ry. Erst zehn Jahre später ist es E. Lieb und dem Autor gelungen, die anfangs gegebene naive Überlegung direkt in exakte Ungleichungen zu fassen und so ein A der richtigen Größenordnung zu gewinnen. Es geht darum, 
oder genauer
![](javascript:ShowPic("/lexika/images/physik/fff7523.jpg", "617", "67");)
(ρ: Elektronendichte) zu beweisen. Der rechts stehende Ausdruck für die kinetische Energie wird in der Thomas-Fermi-Theorie verwendet und sollte demnach eine untere Schranke für die kinetische Energie sein. Wir konnten allerdings (6) nicht mit dem c der Thomas-Fermi-Theorie beweisen, sondern nur mit einer um 4π kleineren Konstante. Vermutlich gilt (6) aber sogar mit der Konstanten der Thomas-Fermi-Theorie, und letztere gibt auch eine untere Schranke für die Gesamtenergie. In diesem Fall erweist sich die physikalische Intuition den Methoden, welche man in Mathematikbüchern findet, überlegen. Dort werden kaum nichtlineare Ausdrücke wie ρ5 / 3 zur Abschätzung von Eigenwerten der linearen Gleichung (3) verwendet.
Zusammenfassend möchte ich die These vertreten, daß in der Physik jeder gute Beweis so weit als möglich den Spuren der Intuition folgen sollte. Umgekehrt ist die Intuition nur gut, wenn sie sich in strenge mathematische Schranken fassen läßt, sonst bleibt sie ein Luftschloß menschlicher Phantasie.
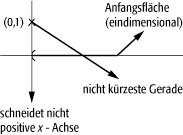
Mathematische Physik 1: Zum Problem der kürzesten Geraden in der Ebene.
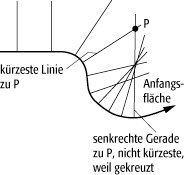
Mathematische Physik 2: Zum Problem der kürzesten Linie zu einer gekrümmten Anfangsfläche.
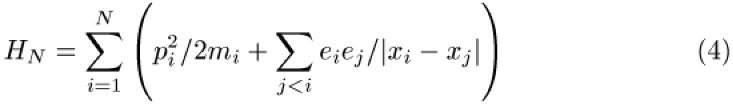
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.