Kombinatorik: Der Stammbaum der Lösungen des Damenproblems
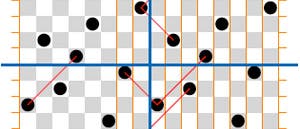
Aufgebracht hat die Frage vor gut 160 Jahren der Schachmeister Max Bezzel (1824 – 1871) aus Ansbach. Mit dem Schachspiel selbst hat das Problem eigentlich nichts zu tun. Schließlich kann es in einer echten Partie nicht vorkommen, dass acht Damen – und sonst keine Figur – auf dem Brett stehen. Abstrakt formuliert lautet das klassische Problem: Man besetze acht der 64 Felder eines Schachbretts derart, dass nirgends in ein und derselben waagerechten, senkrechten oder um 45 Grad geneigten Linie zwei besetzte Felder vorkommen. Damit wird es ein mathematisches Problem.
Auch der große Carl Friedrich Gauß (1777 – 1855) hat sich damit auseinandergesetzt. Im Prinzip kann man es durch erschöpfendes Durchprobieren lösen. Dadurch wird es zur Übungsaufgabe für die Informatiker, die darum wetteifern, die Anzahl der Lösungen auf immer größeren Schachbrettern zu ermitteln. Eine Gruppe aus dem Institut für Informatik der TU Dresden hält gegenwärtig den Rekord mit dem 26 · 26-Brett. Ich selbst bin für die unten beschriebene Variante, das Torus-Damenproblem, bis zur Seitenlänge 31 vorgedrungen...
Schreiben Sie uns!
Beitrag schreiben