Mathematische Unterhaltungen: Kettenwurzeln

Dieser Artikel ist Abonnenten mit Zugriffsrechten für diese Ausgabe frei zugänglich.

Mathematische Unterhaltungen: Kettenwurzeln

Wenn man Wurzeln aus Wurzeln aus Wurzeln zieht, kann diese Art der Wurzelbehandlung gut enden? Das kommt ganz darauf an.

von Christoph Pöppe

Kettenwurzeln — © Christoph Pöppe (Ausschnitt)

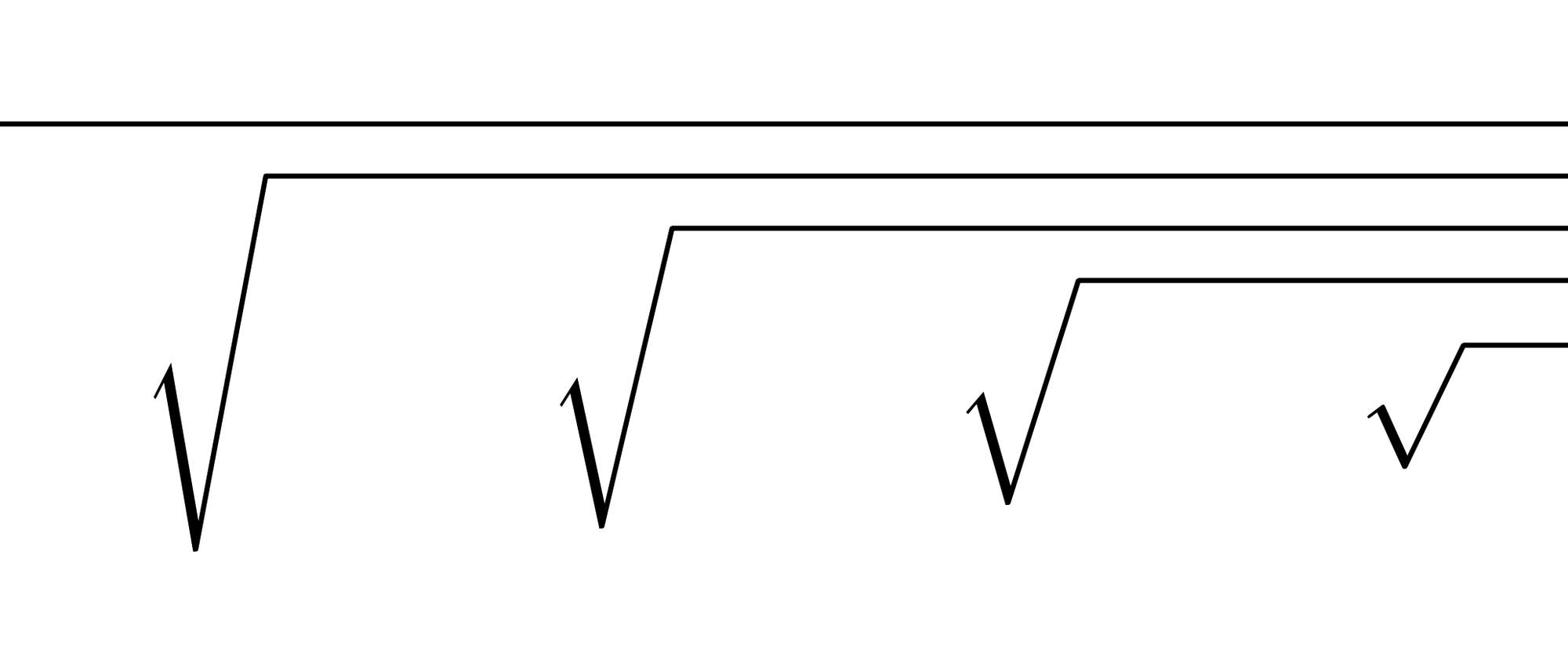
Wie viel ist \[\sqrt{1+ 2\sqrt{1+ 3\sqrt{1+ 4\sqrt{1 + 5\sqrt{1+ \dots}}}}} ?\]

Diese unendliche Kettenwurzel wirkt auf den ersten Blick ungeheuer abschreckend. Man soll eine Wurzel aus etwas ziehen, das wieder eine Wurzel enthält, unter der ein weiteres Wurzelzeichen steckt und so weiter bis ins Unendliche, wie die Pünktchen andeuten. Wie soll das gehen, so dass am Ende eine Zahl als Ergebnis herauskommt? ...

Download (Abo)

Kennen Sie schon …

Spektrum Kompakt – Berühmte Zahlen - Die fabelhafte Welt der Mathematik

Wie klein oder groß sie sein mögen, Zahlen können mit vielen Eigenschaften faszinieren. Einige Kategorisierungen – wie natürlich, rational oder irrational – lernen wir in der Schule. Aber Zahlen können sogar danach unterschieden werden, ob sie fröhlich, traurig, spannend oder langweilig sind.

Spektrum Kompakt – Pi ist überall - Die fabelhafte Welt der Mathematik

Häufiger als man denkt, schleicht sie sich in unseren Alltag ein: Die Kreiszahl Pi spielt nicht nur eine Rolle bei runden Flächeninhalten, sondern auch bei Lebenssimulationen, Streichhölzern oder Billardspielen - und obwohl sie seit jeher fasziniert, wirft ihr Vorkommen noch immer Fragen auf.

Spektrum - Die Woche – Flut in Deutschland

Die verheerende Flutkatastrophe wird uns noch lange Zeit beschäftigen. Doch wie ist das Rekordhochwasser überhaupt zu Stande gekommen? Und können sich Überflutungen künftig verhindern lassen? Das erfahren Sie in dieser Woche.

Quellen

Herschfeld, A.:On Infinite Radicals. In: The American Mathematical Monthly 42, S. 419–429, 1935

Lesher, D., Lynd, C. D.:Convergence Results for the Class of Periodic Left Nested Radicals. In: Mathematics Magazine 89, S. 319–335, 2016

Lynd, C. D., Sharpe, J. W.:Sequences Generated by Powers of the k-th-order Fibonacci Recurrence Relation. In: The American Mathematical Monthly 125, S. 443–446, 2018

Zimmerman, S., Ho, C.:On Infinitely Nested Radicals. In: Mathematics Magazine 81, S. 3–15, 2008

Die Ramanujan-Kettenwurzel, Aufgabe

Die Ramanujan-Kettenwurzel, Lösung

Jamie Johnson, Tom Richmond: Continued Radicals

Brian Thomas: On infinitely nested radicals. Paraphrase von Zimmerman/Ho.

Pierluigi Vellucci, Alberto Maria Bersani: New formulas for \(\pi\) involving infinite nested square roots and Gray code.

Schreiben Sie uns!

Beitrag schreiben

Beitrag darf veröffentlicht werden

Wir freuen uns über Ihre Beiträge zu unseren Artikeln und wünschen Ihnen viel Spaß beim Gedankenaustausch auf unseren Seiten! Bitte beachten Sie dabei unsere Kommentarrichtlinien.

Tragen Sie bitte nur Relevantes zum Thema des jeweiligen Artikels vor, und wahren Sie einen respektvollen Umgangston. Die Redaktion behält sich vor, Zuschriften nicht zu veröffentlichen und Ihre Kommentare redaktionell zu bearbeiten. Die Zuschriften können daher leider nicht immer sofort veröffentlicht werden. Bitte geben Sie einen Namen an und Ihren Zuschriften stets eine aussagekräftige Überschrift, damit bei Onlinediskussionen andere Teilnehmende sich leichter auf Ihre Beiträge beziehen können. Ausgewählte Zuschriften können ohne separate Rücksprache auch in unseren gedruckten und digitalen Magazinen veröffentlicht werden. Vielen Dank!