Quantenphysik: Unschärfe unter Beweis gestellt
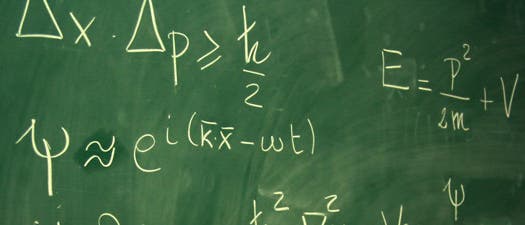
Das Sonderbare der Quantenmechanik lässt sich in einer einzigen Formel zusammenfassen: der Unschärferelation. Den Lehrbüchern zufolge besagt sie, dass es prinzipiell unmöglich ist, die genaue Position und den Impuls eines subatomaren Teilchens zu kennen - je genauer man die Position des Teilchens zu einem bestimmten Zeitpunkt kennt, desto weniger weiß man über den Wert des Impulses.
Die ursprüngliche Formulierung des Prinzips, das der Physiker Werner Heisenberg im Jahr 1927 aufstellte, beschreibt jedoch die Unbestimmtheit auf anderem Wege - als die fundamentale Grenze, mit der ein Messapparat Quantenzustände ausmessen kann. Heisenberg lieferte keinen direkten Beweis für diese Formulierung des Prinzips und äußerte seine Ideen "bloß informell und intuitiv", erzählt der Physiker Jos Uffink von der University of Minnesota in Minneapolis.
Nun glauben Forscher endlich einen formalen Beweis gefunden zu haben. "Unsere Arbeit belegt, dass man nichts mit höherer Genauigkeit messen kann, als es die fundamentale Unschärfe erlaubt", sagt Paul Busch, theoretischer Physiker an der University of York, der mit seinen Kollegen den Beweis am 6. Juni auf arXiv vorab veröffentlichte [1]. Damit stellen sie nicht nur die Rolle des Messvorgangs in der quantenmechanischen Unbestimmtheit auf eine solide Grundlage - eine Rolle, die Physiker bereits anzuzweifeln begannen - sondern sie liefert zusätzlich einen Hinweis, dass mittels Quantenkryptografie verschlüsselte Nachrichten abhörsicher übermittelt werden können.
Theoretische Messung
In ihrer theoretischen Arbeit betrachteten Busch und Kollegen Messungen, in denen gleichzeitig Ort und Impuls eines Teilchens in einem beliebigen Quantenzustand bestimmt werden. Die Genauigkeit dieser Messungen verglichen sie dann mit zwei Spezialfällen, in denen entweder der Ort oder der Impuls des Teilchens genau bekannt ist. Es stellte sich heraus, dass in den beiden Spezialfällen die zusammengefasste Genauigkeit in der Positions- und Impulsmessung zum einen der heisenbergschen Relation gehorcht und zum anderen immer höher ist als in Messungen, in denen beide Größen gleichzeitig bestimmt wurden. Dieser Schritt erlaubte es ihnen, Heisenbergs ursprüngliche Vermutung zu beweisen.
Die Arbeit von Busch und seinen Koautoren "sollte man sich merken", meint der Mathematiker Hans Maassen von der Radboud-Universität in Nimwegen. "Es ist gut möglich, dass sie in den Lehrbüchern bald als die eigentlich korrekte Formulierung von Heisenbergs Unschärferelation dargestellt wird." Doch andere Kollegen sind weniger zuversichtlich, denn der Beweis hat eine zehn Jahre alte Debatte neu entfacht.
Hitzige Debatte
Im Jahr 2003 stellte der Physiker Masanao Ozawa, der mittlerweile an der Nagoya Universität in Japan forscht, die These auf, dass die Interpretation der heisenbergschen Unschärferelation, die die Unbestimmtheit des Systems auf den Messvorgang zurückführt, verletzt werden könnte. Ozawas Theorie wurde 2004 veröffentlicht [2] und im letzten Jahr erhärtet, als ein Team um Aephraim Steinberg und Lee Rozema von der University of Toronto die Ergebnisse eines Experiments vorstellten, in dem sie die Polarisation eines einzelnen Photons entlang zweier senkrechter Richtungen bestimmten [3].
"Diese Arbeit sollte man sich merken."Hans Maassen
Wie bei Position und Impuls sagt die Quantentheorie voraus, dass man die Polarisation entlang zweier unterschiedlicher Achsen nicht gleichzeitig präzise kennen kann. Das Team wendete nun eine besondere Strategie an, bei der die Polarisation zunächst durch eine Reihe "schwacher" Messungen untersucht wird. In diesem Fall wird das System kaum gestört, die Messung muss allerdings mehrmals wiederholt werden, um die gleiche Information zu liefern, die eine einzige "starke" Messung liefern kann. Sie fanden heraus, dass die Polarisationsmessungen das System im Mittel nur halb so stark störten, wie es Heisenbergs ursprüngliche Formulierung der Unschärferelation vorgibt.
Ozawa glaubt, dass Busch und Kollegen, um zu ihrem Ergebnis zu kommen, den denkbar ungünstigsten Fall annahmen und über viele Quantenzustände mittelten, um die Störung durch einen Messapparat zu charakterisieren. Dies entspricht womöglich gar nicht den Bedingungen, unter denen ein bestimmtes Quantensystem in einem bestimmten Quantenzustand tatsächlich untersucht wird. Nach Ozawa überschätzen sie folglich die Messunsicherheit. Busch und seine Kollegen hingegen argumentieren, dass die von Ozawa genutzte Definition von Messfehlern nicht allgemeingültig ist und daher Heisenbergs Formulierung nicht in Frage stellen kann.
Kryptische Verbindung
Die Debatte mag weltfremd klingen, doch für alle, die sich mit Quantenkryptografie und Quantencomputern auseinandersetzen, ist die Frage, inwieweit ein Messapparat die Eigenschaften eines Quantensystems beeinflusst, von zentraler Bedeutung. Im Prinzip wäre ein Quantencomputer sicherer als ein gewöhnlicher Computer, denn jeder, der Informationen ausspähen möchte, würde eine verräterische Spur hinterlassen.
Sollte sich jedoch Ozawas Hypothese von 2004 erhärten, könnte ein Dieb in der Lage sein die (Quanten-)Daten abzufangen, ohne bemerkt zu werden, da die heimliche Messung das System insgesamt kaum beeinflusst.
Laut Uffink haben Busch und Kollegen jedoch immerhin nachgewiesen, dass der Lauscher das System zwangsläufig so beeinflussen wird, wie es die ursprüngliche Formulierung der Unschärferelation voraussagt - sofern er keine Kontrolle über den Zustand des Quantensystems hat, was bei einem Datendieb in der Regel der Fall sein sollte. "Das ist eine wichtige Erkenntnis, die wir bislang noch nicht hatten", meint Uffink.
Weder Uffink noch der Quantentheoretiker Howard Wiseman von der Griffith University in Brisbane würden jedoch so weit gehen und behaupten, dass Ozawa mit seinem Ansatz falsch liegt. Tatsächlich könnten beide Ergebnisse korrekt sein, betont Wiseman.
Er vermutet hinter dem Problem ein eigenartiges quantenmechanisches Konzept, das man als negative Wahrscheinlichkeit bezeichnet: ein Bereich, in dem die Wahrscheinlichkeitsverteilung von Position oder Impuls eines Teilchens einen negativen Wert annimmt. Diese Eigenschaft könnte dazu führen, dass ein Messapparat das System weniger stark stört, als es die Unschärferelation vordergründig zu erlauben scheint.
Dieser Umstand, dass die beiden verschiedenen Definitionen verschiedene Antworten liefern, "zeigt doch ganz gut, wie verrückt die Quantenmechanik tatsächlich ist", sagt Wiseman.
Dieser Artikel erschien unter dem Titel "Proof mooted for quantum uncertainty" in Nature 498, S. 419–420, 2013.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.