Hemmes mathematische Rätsel: Auf wie viele Weisen kann der Würfel gefärbt werden?
Im Januar 1968 erschien die erste Ausgabe der Zeitschrift »Journal of Recreational Mathematics«, die sich ausschließlich mit der Unterhaltungsmathematik befasst. S2001 stellte Brian Barwell, ein britischer Ingenieur und Erfinder zahlreicher Denksportaufgaben, den Lesern und Leserinnen folgendes Problem vor.
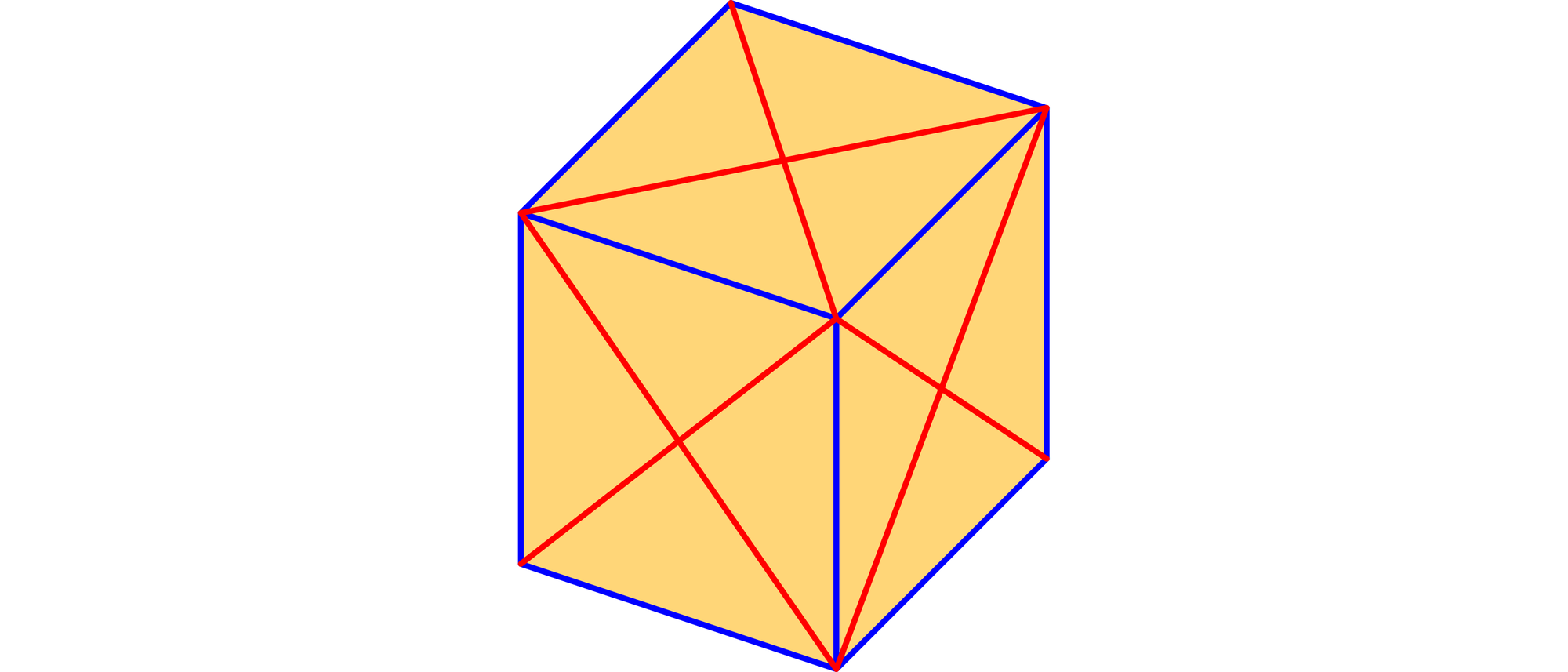
Alle sechs Seitenflächen eines Würfels sind durch ihre Diagonalen in jeweils vier Dreiecke unterteilt worden. Die 24 Dreiecke der Würfeloberfläche sollen jetzt rot, gelb, grün und blau gefärbt werden, so dass auf jeder Fläche alle vier Farben vorkommen und an jeder Kante des Würfels nur gleichfarbige Dreiecke aneinanderstoßen. Auf wie viele Weisen kann der Würfel gefärbt werden? Würfelfärbungen, die durch Drehungen und Spiegelung ineinander übergehen, zählen nicht als unterschiedlich.
In der einer Zeichnung einer Würfelabwicklung sind die 24 Flächendreiecke mit den Buchstaben A bis L gekennzeichnet, wobei jeweils zwei Dreiecke, die an einer Kante zusammenstoßen, den gleichen Buchstaben tragen.
Falls das Dreieck A der Würfeloberseite ABCD blau ist, sind insgesamt die folgenden verschiedenen Färbungen dieser Würfelfläche möglich. Alle anderen denkbaren Färbungen erhält man durch Vertauschen der Farben.
Angenommen, die Würfeloberseite hat die erste der sechs Färbungen, dann kann E nur gelb oder rot sein. Nehmen wir zunächst einmal an, E sei gelb. Nun lässt sich der Würfel nur noch auf eine einzige Art nacheinander weiterfärben, so dass keine Farbe auf einer Fläche doppelt vorkommt. Auch wenn andererseits E rot ist, kann man die Flächen des Würfels nur auf eine einzige Weise färben, wobei man aber dabei nur ein spiegelbildliches Muster der ersten Färbung erhält.
Betrachtet man den gefärbten Würfel genauer, erkennt man, dass jede der sechs möglichen Färbungen für die Seitenflächen genau einmal vorkommt. Damit ergeben die möglichen Farbvertauschungen der Würfeloberseite keine neuen Färbungen mehr, sondern sie lassen sich alle durch Drehen des Würfels erzeugen. Folglich hat das Problem, bis auf die Vertauschung der Farben, nur eine einzige Lösung.
Schreiben Sie uns!
Beitrag schreiben