Coolidge
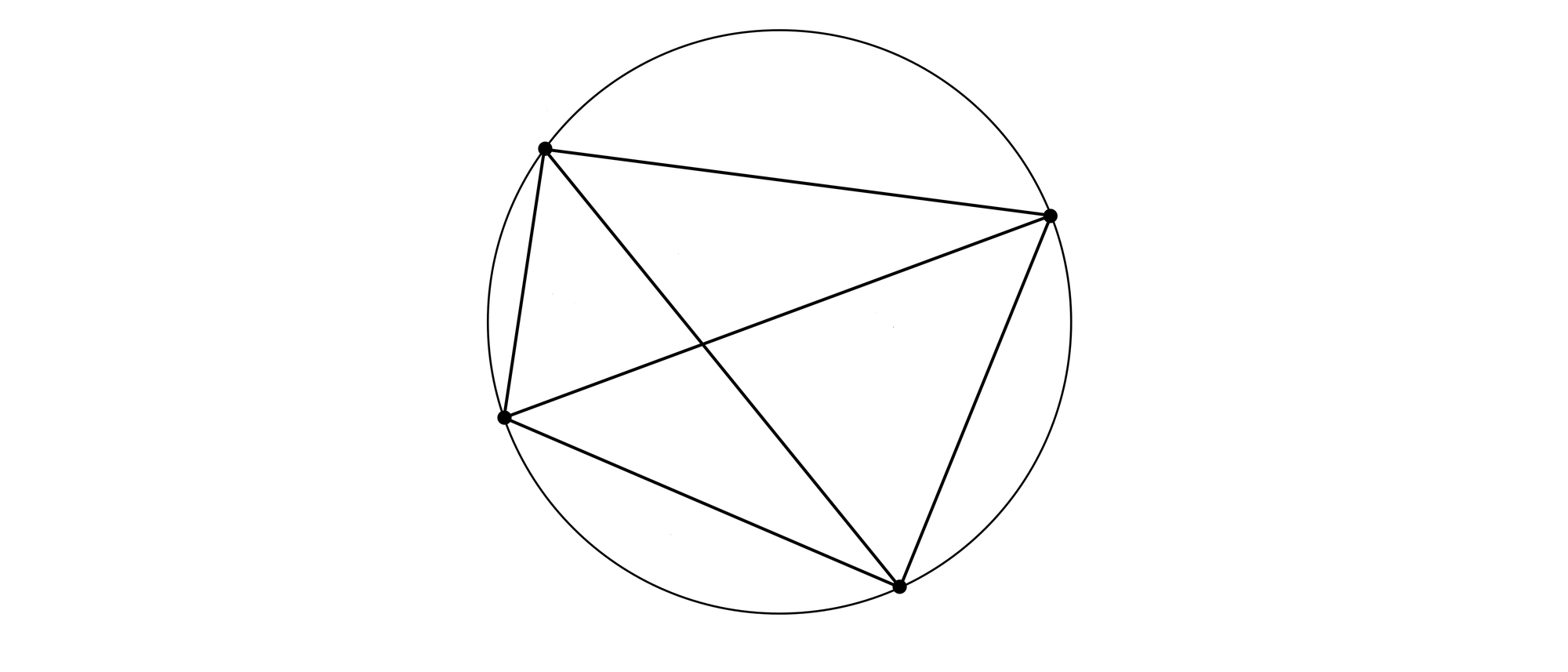
Wir wählen vier Punkte auf einem Kreis und machen sie (durch Weglassen jeweils eines Punktes) zu den Ecken von vier verschiedenen Dreiecken, die somit einen gemeinsamen Umkreis haben. Zeigen Sie bitte:
1. Die Schwerpunkte der vier Dreiecke liegen auf einem Kreis.
2. Die Höhenschnittpunkte liegen ebenfalls auf einem Kreis (aber einem anderen als bei 1.).
3. In einem Dreieck heißt der Kreis durch die Höhenfußpunkte und die Seitenmitten "Neunpunktekreis". Die Mittelpunkte der Neunpunktekreise liegen auch auf einem Kreis, und in dessen Mittelpunkt schneiden sich alle vier Neunpunktekreise.
Was kann man über die Radien und die Lagen der Mittelpunkte der genannten Kreise sagen?
Im Dreieck wird die Strecke zwischen Höhenschnittpunkt und Umkreismittelpunkt (Euler-Gerade) vom Mittelpunkt des Neunpunktekreises und dem Schwerpunkt im Verhältnis 3:1:2 geteilt. Das Viereck aus den Schwerpunkten der vier Dreiecke ist ähnlich zu dem Viereck der Ecken.
Die großen schwarzen Kleckse sind die vier Ecken, die blauen sind die Schwerpunkte der vier Dreiecke und des Vierecks. Letzterer teilt die Verbindung eines jeden Dreiecks-Schwerpunktes mit der "fehlenden" Ecke im Verhältnis 1:3. Also ist jeder Dreiecks-Schwerpunkt das Bild der fehlenden Ecke unter einer zentrischen Streckung mit dem Faktor –1/3 bezüglich des Vierecks-Schwerpunkts.
Demnach liegen die Dreiecks-Schwerpunkte auf einem Kreis, wenn die vier Ecken auf einem liegen, allerdings ist der Schwerpunkt aller 4 Ecken im Allgemeinen nicht dessen Mittelpunkt.
Aus dem für alle vier Dreiecke gemeinsamen Umkreis-Mittelpunkt und den vier Schwerpunkten können die übrigen Punkte der Euler-Geraden (blau) durch Streckungen in den angegebenen Verhältnissen konstruiert werden. Damit liegen auch die Mittelpunkte der Neunpunktekreise (rot) auf einem Kreis (rot gestrichelt), ebenso die Höhenschnittpunkte (grün). Die Radien dieser Kreise sind halb so groß bzw. genau so groß wie der für alle gemeinsame Umkreisradius.
Die Mittelpunkte des Umkreises und der Kreise durch (a) die Schwerpunkte (blau gestrichelt), (b) die Mittelpunkte der Neunpunktekreise (rot gestrichelt) und (c) die Höhenschnittpunkte (grün) liegen also auch auf einer Geraden, die von diesen Punkten ebenso wie die Euler-Gerade im Verhältnis 3:1:2 geteilt wird. Sie ist gewissermaßen die Euler-Gerade für das (Sehnen-)Viereck.
Der Satz von Coolidge (in Honsbergers "Chestnuts" auf Seite 239) ist sozusagen eine Verallgemeinerung einer Teilaussage dieser Aufgabe: Man kann für jedes n-Eck einen verallgemeinerten Neunpunktekreis-Mittelpunkt definieren. Die so definierten Mittelpunkte aller (n–1)-Ecke eines n-Ecks liegen dann auch auf einem Kreis.
Schreiben Sie uns!
Beitrag schreiben