Hemmes mathematische Rätsel: Das Rätsel des Schildkrötenpanzers
Choi Seok-jeong lebte von 1646 bis 1715 und war ein koreanische Politiker und Mathematiker der Joseon-Ära. Im Jahr 1700 erschien sein Buch »Gusuryak«. Darin findet man unter anderem die weltweit erste Veröffentlichung über lateinische Quadrate. Fälschlicherweise wird ihre Erfindung meistens dem Schweizer Mathematiker Leonhard Euler zugeschrieben, der sie aber erst 67 Jahre später beschrieb. In dem Buch »Gusuryak« stellt Choi Seok-jeong auch sein Schildkrötenpanzerrätsel vor.
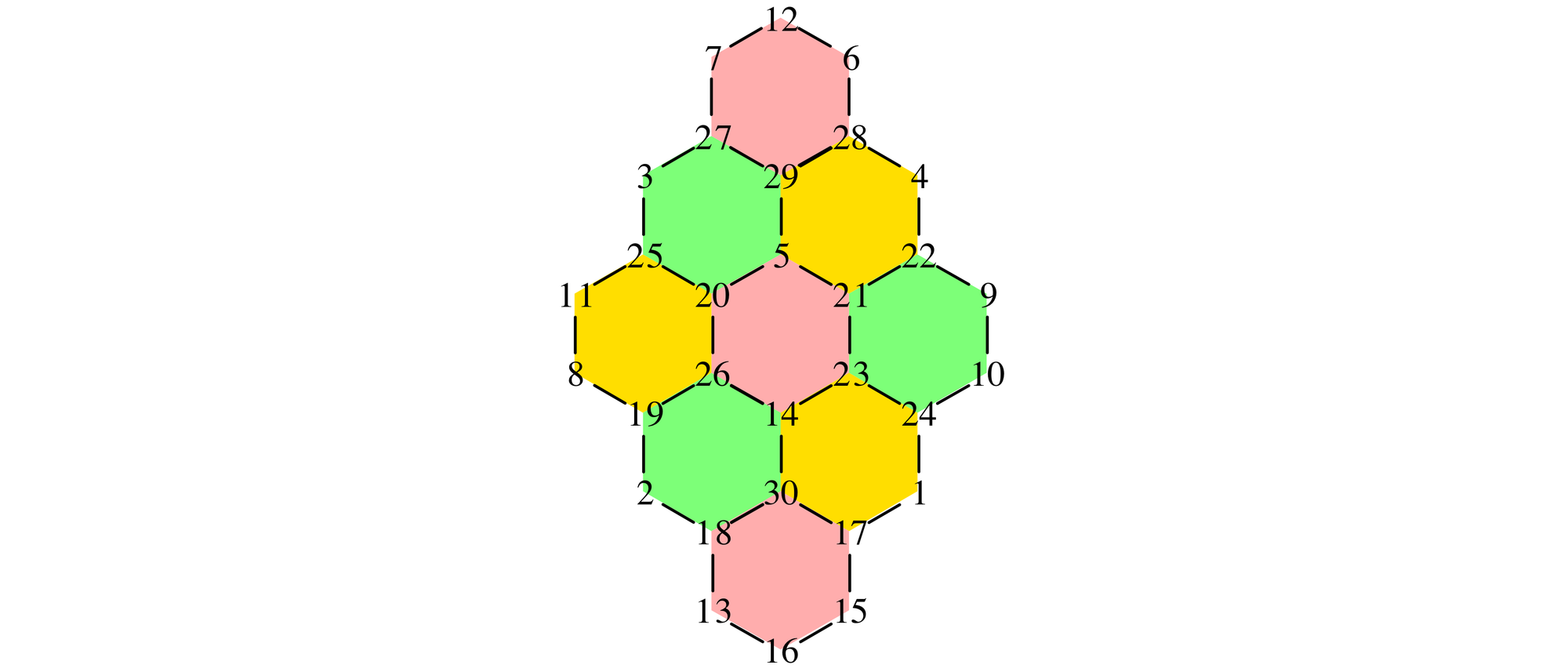
Auf die 30 Ecken eines Rasters aus neun Sechsecken, das an das Muster eines Schildkrötenpanzers erinnert, sollen die Zahlen von 1 bis 30 verteilt werden. Dabei soll die Summe der sechs Zahlen auf den Ecken eines jeden Sechsecks gleich sein. Choi Seok-jeong hat eine Lösung mit einer Sechsecksumme von 93 angegeben. Sie kann auch andere Werte haben, aber höchstens 109 betragen. Die Abbildung zeigt ein Beispiel hierfür. Bestimmen Sie die kleinstmögliche Sechsecksumme, und finden Sie eine Beispiellösung dafür.
Tauscht man jede Zahl a in dem Muster gegen die Zahl 31 − a aus, enthält es, wie auch schon zuvor, alle Zahlen von 1 bis 30 nur eben in umgekehrter Reihenfolge. Die Sechsecksumme beträgt jetzt aber (31 − a1) + (31 − a2) + (31 − a3) + (31 − a4) + (31 − a5) + (31 − a6) = 6 · 31 − (a1 + a2 + a3 + a4 + a5 + a6). Da die Summe der Zahlen von a1 bis a6 laut Aufgabe maximal 109 sein kann, ist der kleinstmögliche Wert der Sechsecksumme = 6 · 31 − 109 = 77. Ein Beispiel hierfür erhält man, indem man jede Zahl a in dem Beispiel aus der Aufgabe durch die Zahl 31 − a ersetzt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.