Hemmes mathematische Rätsel: Der Mittelwertswürfel
Eugene B. Dynkin wurde 1924 in St. Petersburg geboren. Er war jüdischer Abstammung, und sein Vater wurde 1935 zum Volksfeind erklärt und in die Verbannung nach Kasachstan geschickt, wo er zwei Jahre später starb. Trotz dieser Vorbelastungen durfte er in Moskau Mathematik studieren. Nach Stalins Tod bekam er sogar eine Professur. 1976 emigrierte er in die USA und wurde 1977 Mathematikprofessor an der Cornell-Universität. 1965 veröffentlichte Dynkin gemeinsam mit S. A. Molchanov, A. L. Rozental und A. K. Tolpygo ein Büchlein mit Problemen der Unterhaltungsmathematik, das 1969 ins Englische übersetzt wurde und unter dem Titel »Mathematical Problems: An Anthology« erschien. Daraus stammt das folgende Rätsel.
Angenommen, auf jeder der acht Ecken eines Würfels stünde eine Zahl. Unter diesen acht Zahlen sind mindestens eine Null und mindestens eine Eins. Nun wird jede Zahl auf den Würfelecken durch den Mittelwert der ursprünglichen Zahlen ersetzt, die auf den drei Nachbarecken stehen, das heißt, auf den Ecken, die durch eine Kante mit ihr verbunden sind. Dieses Ersetzen aller Zahlen durch die Mittelwerte wird zehnmal nacheinander durchgeführt. Danach stehen auf den Würfelecken wieder die gleichen Zahlen wie am Anfang. Ist dies möglich, und wenn ja, welche Zahlen haben ursprünglich auf dem Würfel gestanden?
Angenommen, nach dem i-ten Ersetzungsschritt wäre die größte Zahl auf den Würfelecken Mi und die kleinste mi. Da Mi und mi durch Mittelwertbildung von Zahlen des Würfels nach dem (i−1)-ten Schritt entstehen, muss Mi kleiner oder gleich Mi−1 sein und mi größer oder gleich mi−1.
Es gilt somit, dass M0 größer oder gleich M1 sein muss, M1 größer oder gleich M2 usw. Außerdem gilt, dass m0 kleiner oder gleich m1 sein muss, m1 kleiner oder gleich m2 und so weiter. Da bei dem Würfel die Beschriftungen zu Anfang und am Ende gleich sind, muss M0 = M10 und m0 = m10 sein.
Das bedeutet aber M0 = M1 = M2 = … = M10 und m0 = m1 = m2 = … = m10. Wenn nach einem Schritt auf einer Ecke die Maximalzahl M0 steht, muss auf jeder der drei benachbarten Ecken vor dem Schritt auch M0 gestanden haben. Wäre das nicht so, müsste bei der Mittelwertbildung mindestens eine der Zahlen größer als M0 gewesen sein, was aber nicht möglich ist.
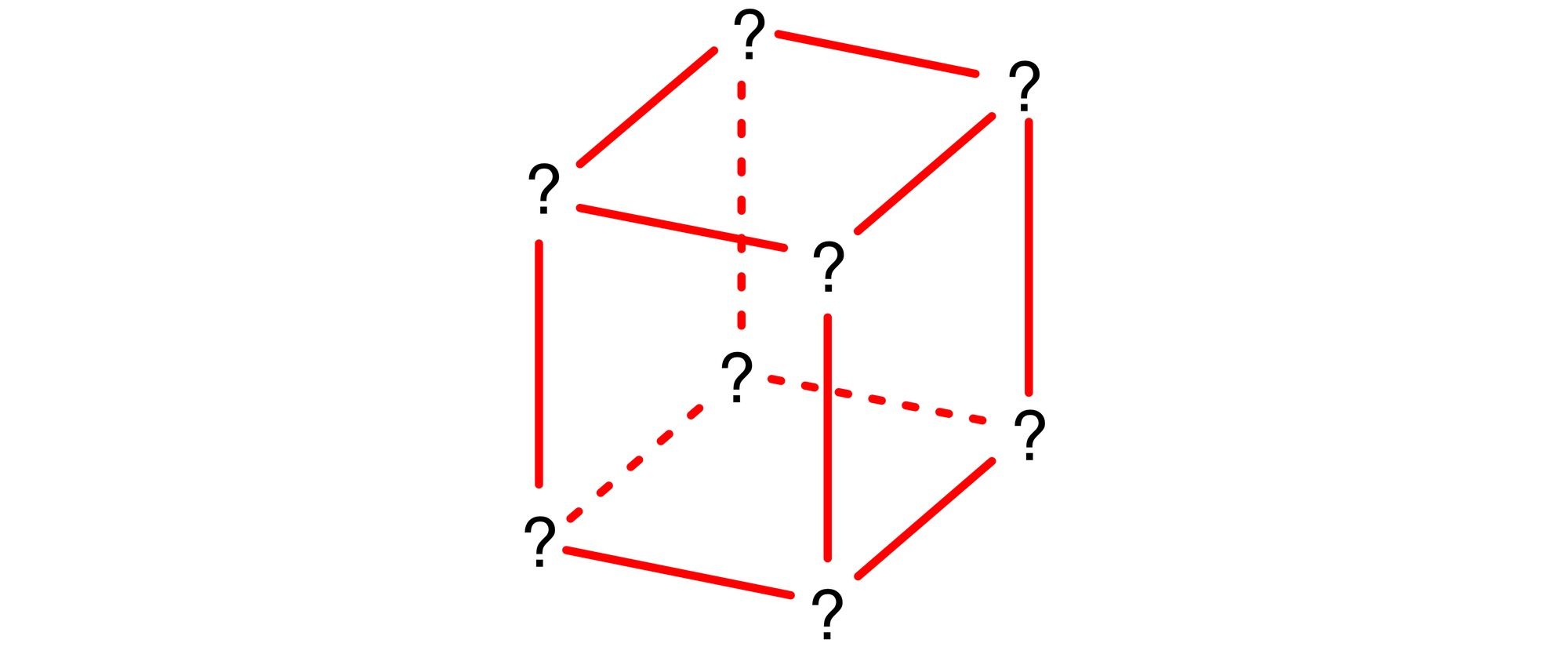
Geht man noch einen Schritt weiter zurück, müssen zuvor alle Nachbarn dieser drei Maximalzahlen M0 gewesen sein, was nur möglich ist, wenn mindestens vier nicht benachbarte Ecken M0 tragen. Aus analogen Gründen müssen mindestens vier nicht benachbarte Ecken m0 tragen. Da mindestens eine 0 und eine 1 vorkommen, gilt M0 = 1 und m0 = 0.
Die Skizze zeigt die einzig mögliche Anordnung. Bei jedem Schritt werden die Einsen zu Nullen und umgekehrt. Nach jeder geraden Schrittanzahl, also auch nach zehn Schritten, ist der Urzustand wieder hergestellt.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.