Hemmes mathematische Rätsel: Die Dreiecke des Sterns
Presh Talwalkar hat Mathematik und Wirtschaftswissenschaften an der Stanford University in Kalifornien in der USA studiert. Er hat einige Bücher über mathematische Knobeleien geschrieben, darunter das 2015 erschienene dreibändige Werk »Math Puzzles«. Aus dem dritten Band stammt die folgende Aufgabe, von der er schreibt, er habe sie von jemanden namens Danny erhalten.
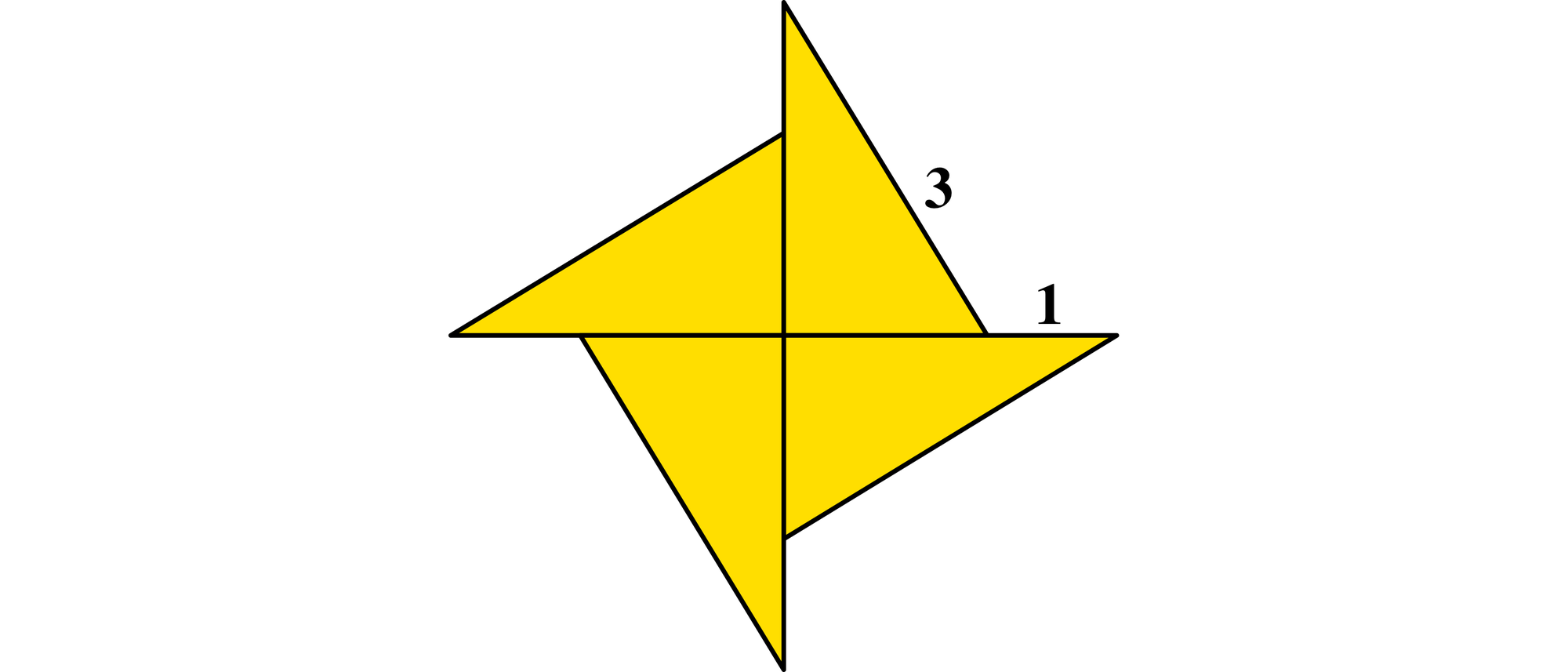
Ein Stern, dessen Seiten die Längen 1 und 3 haben, ist aus vier gleichen rechtwinkligen Dreiecken zusammengesetzt. Wie groß ist die Fläche jedes dieser Dreiecke?
Natürlich kann man das Problem lösen, indem man den Satz des Pythagoras anwendet und eine quadratische Gleichung aufstellt und löst, aber es geht auch viel einfacher. Zieht man die vier Dreiecke so weit auseinander, dass sich ihre Spitzen gegenseitig berühren, bilden sie ein Quadrat mit einem quadratischen Loch im Inneren. Nun ist es sehr leicht, die Fläche eines Dreiecks zu berechnen: A = ¼(32 – 12) = 2.
Schreiben Sie uns!
Beitrag schreiben