Hemmes mathematische Rätsel: Die Innenwinkel eines Polygons
Es gab Zeiten, da lag das Niveau der Werbung deutlich über dem der Sätze »Geiz ist geil« und »Ich bin doch nicht blöd«. Zwischen 1959 und 1971 warb die Firma Litton Industries in den Zeitschriften Aviation Week und Electronic News für ihre Produkte mit Anzeigen, die jedes Mal eine mathematische Denksportaufgabe enthielten. Diese Aufgaben waren ein so großer Erfolg, dass Litton Industries sie in gesammelter Form als eine Reihe kleiner Hefte mit dem Titel Problematical Recreations herausgab. Später erschienen die besten dieser Probleme noch einmal in den von Angela Dunn herausgegeben Büchern Mathematical Bafflers (1964) und Second Book of Mathematical Bafflers (1983) und in dem Buch Litton's Problematical Recreations (1971), das James F. Hurley herausgab. Die beiden ersten Bücher sind auch heute noch im Buchhandel erhältlich. Am 2. Januar 1967 erschien in Electronic News folgende Aufgabe:
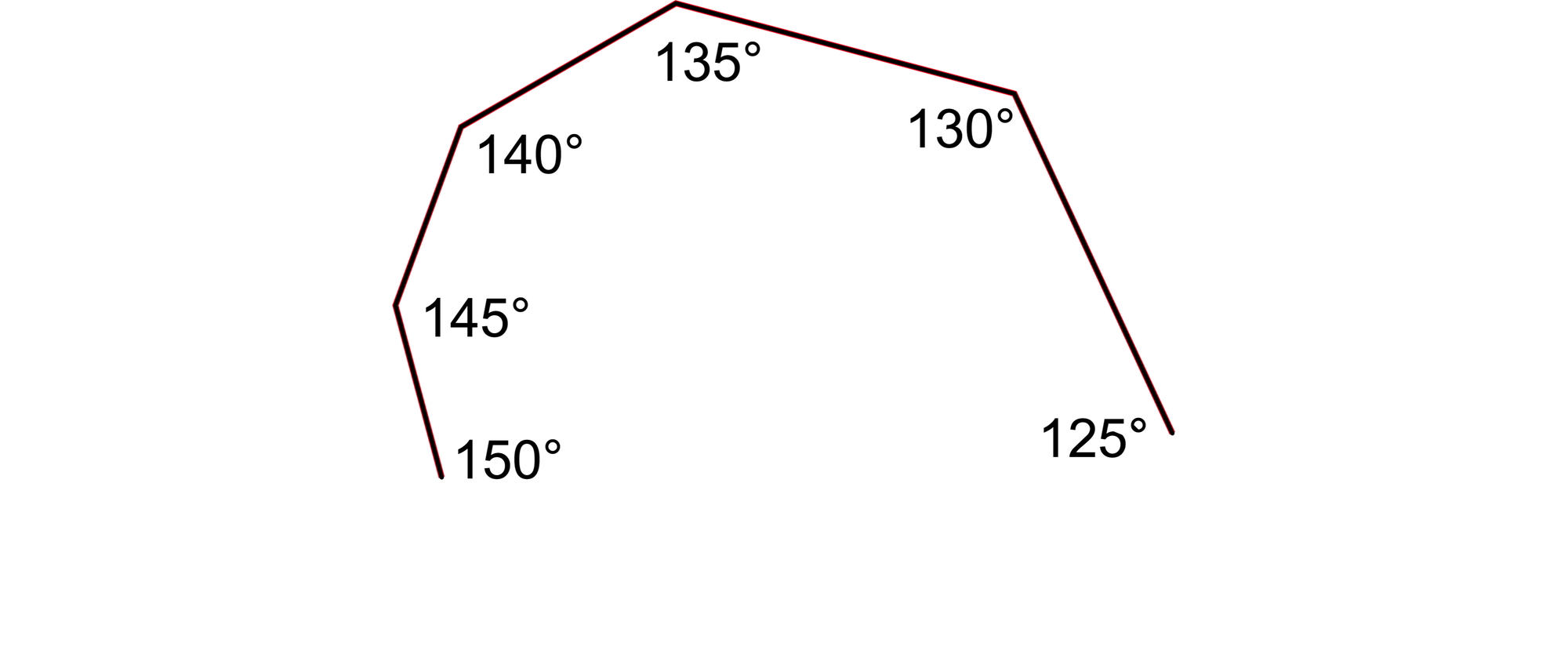
Der kleinste Innenwinkel eines ebenen Vielecks ist 120° groß. Alle weiteren Innenwinkel des Polygons nehmen gegen den Uhrzeigersinn gesehen stets um 5° zu. Der zweite Innenwinkel ist also 125 Grad groß, der dritte 130 Grad, der vierte 135 Grad und so weiter. Wie viele Ecken kann das Polygon haben?
Die Summe der Innenwinkel jedes ebenen n-Eck beträgt (n – 2)•180°.
Die Innenwinkel des n-Ecks aus der Aufgabe bilden eine arithmetische Reihe mit dem Anfangsglied a1 = 120°, der Differenz zwischen benachbarten Gliedern d = 5° und der Gliederzahl n. Nach der Formel für die Reihensumme a1n + n(n – 1)d/2 beträgt die Summe der Innenwinkel 120°•n + n(n – 1)•5°/2.
Diese beiden Ausdrücke für die Winkelsumme werden gleichgesetzt und ergeben (n – 2)•180° = 120°•n + n(n – 1)•5°/2. Die Gleichung lässt sich zu n2 – 25n + 144 = 0 vereinfachen. Sie ist quadratisch und hat die beiden Lösung n = 9 und n = 16.
Wie solche Neunecke und Sechszehnecke mit den passenden Winkeln aussehen könnten, zeigen die Skizzen. Ob man n = 16 überhaupt als Lösung akzeptiert, ist Ansichtssache, denn einer der sechzehn Winkel von 120° bis 195° ist 180° groß, ist also ein gestreckter Winkel. Die beiden Seiten des Sechzehnecks, die ihn einschließen, liegen darum auf einer geraden Linie. Somit ist das Polygon tatsächlich nur ein Fünfzehneck.
Schreiben Sie uns!
Beitrag schreiben