Hemmes mathematische Rätsel: Die Reise auf dem Rhombendodekaeder
Harold Scott MacDonald Coxeter war ein britisch-kanadischer Mathematiker. Er wurde 1907 in London geboren und starb 2003 in Toronto. Coxeter war über Jahrzehnte die führende Autorität der klassischen Geometrie, worüber er bekannte Lehrbücher verfasste. Er betrieb geometrische Forschung zu einer Zeit, als die Geometrie als altbacken belächelt wurde und sich kaum ein Mathematiker damit ernsthaft befasste. Coxeter interessierte sich auch sehr für die Unterhaltungsmathematik. 1946 veröffentlichte er in der Zeitschrift American Mathematical Monthly eine hübsche Denksportaufgabe.
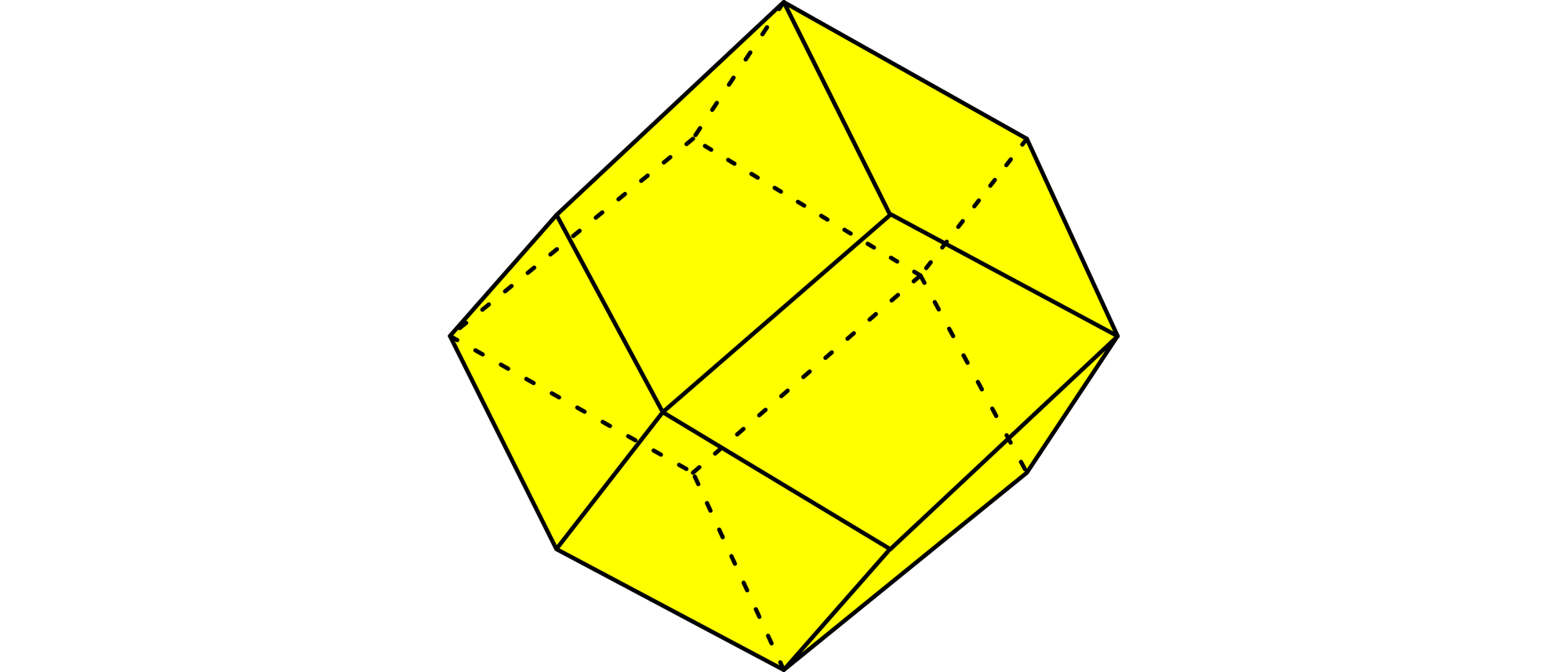
Ein Rhombendodekaeder ist ein Körper, der vierzehn Ecken hat und von zwölf gleichen Rhomben begrenzt wird. Auf einer Ecke dieses Polyeders sitzt eine Spinne und kriecht von dort aus nacheinander zu allen anderen 13 Ecken. Sie bewegt sich nur entlang der Kanten des Körpers und überquert keine Ecke mehrmals. Wie viele verschiedene Wege kann die Fliege nehmen?
Für die Aufgabe spielt die genaue dreidimensionale Form des Rhombendodekaeders gar keine Rolle. Wichtig sind nur die Verbindungen der Ecken durch die Kanten. Darum reicht es aus, eine Projektion des Körpers auf die Ebene zu betrachten, die in der Mathematik als Schlegeldiagramm bezeichnet wird.
Die grünen Kreise stellen dabei die Ecken mit drei Kanten dar, die roten die mit vier Kanten. Die Verbindungslinien sind Bilder der Kanten. Jede dreikantige Ecke hat als Nachbarn nur vierkantige Ecken; von einer dreikantigen Ecke kann also die Spinne als nächste nur vierkantige Ecken erreichen. Die Nachbarn der vierkantigen Ecken sind umgekehrt alle dreikantig. Die Spinne muss auf ihrer Tour folglich immer abwechselnd zu einer drei- und einer vierkantigen Ecke kriechen. Das Rhombendodekaeder hat jedoch sechs vierkantige und acht dreikantige Ecken, und die lassen sich nicht alle abwechselnd aneinander reihen. Somit gibt es keine Lösung.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.