Hemmes mathematische Rätsel: Die Schnittpunkte der Diagonalen
Paul Erdős wurde 1913 in Budapest geboren und starb 1996 in Warschau. Er war einer der bedeutendsten Mathematiker des 20. Jahrhunderts. Erdős arbeitete ständig weltweit mit Hunderten von Kollegen zusammen auf den Gebieten der Kombinatorik, der Graphentheorie und der Zahlentheorie. Darum war er stets unterwegs und lebte nur aus dem Koffer. Von ihm stammt die Idee von dem BUCH, in dem Gott die perfekten Beweise für mathematische Sätze aufbewahrt. Ein Versuch, diesem Buch nahezukommen, stellt Das BUCH der Beweise dar, das 1998 mit seiner Einwilligung veröffentlicht wurde. 1946 stellte er in der Zeitschrift The American Mathematical Monthly das folgende Problem vor:
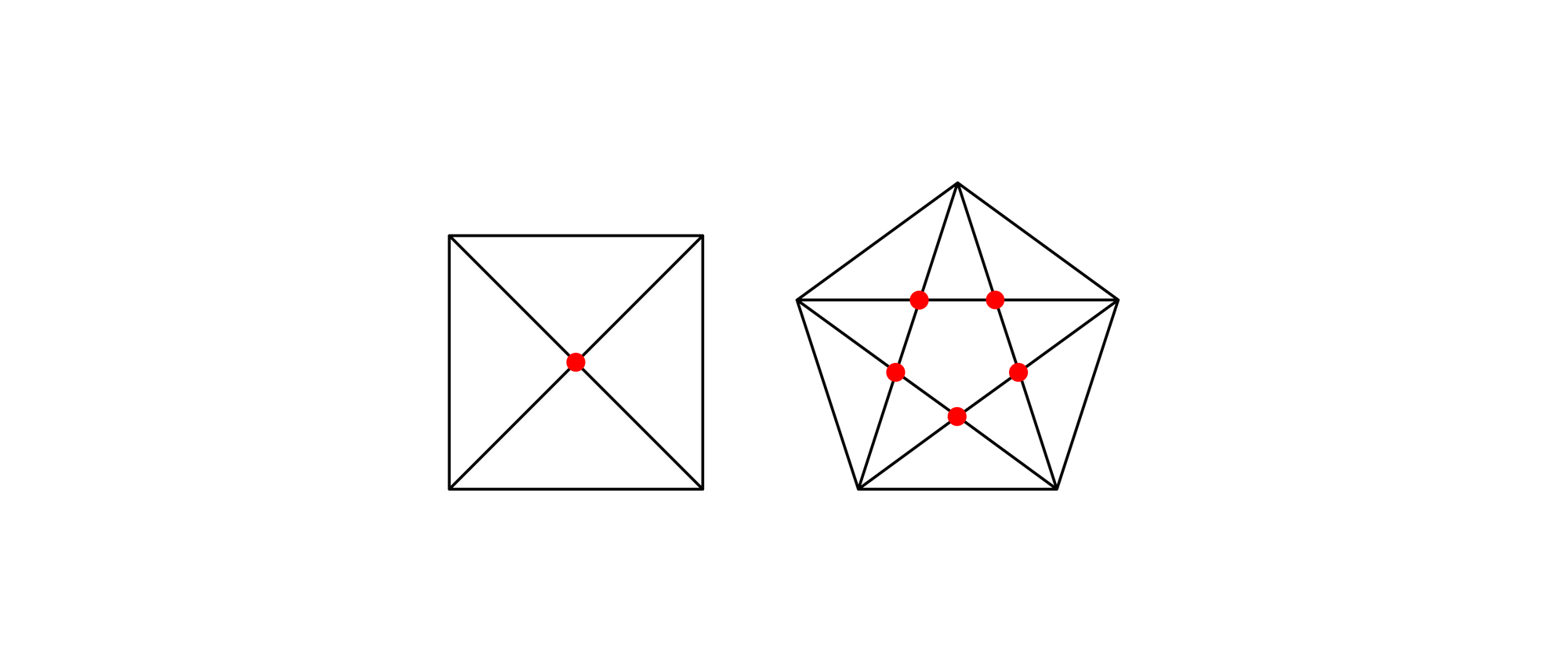
Als Diagonalen bezeichnet man in einem n-Eck die Verbindungsstrecken der Eckpunkte untereinander. Dabei zählen die Seiten des n-Ecks nicht mit. Bei einem Quadrat schneiden sich die Diagonalen in einem Punkt und bei einem regelmäßigen Fünfeck in fünf Punkten. Wie viele Diagonalenschnittpunkte kann es in einem konvexen, aber nicht unbedingt regelmäßigen n-Eck höchstens geben?
Ein Dreieck hat keine Diagonalen und somit auch keine Schnittpunkte von Diagonalen. Bei einem konvexen n-Eck mit vier oder mehr Seiten kann man sich jede beliebige Auswahl von vier Ecken als die Eckpunkte eines Vierecks vorstellen.
Dieses Viereck hat zwei Diagonalen, die sich in einem Punkt schneiden. Umgekehrt gehört zu jedem sich schneidenden Paar von Diagonalen genau ein Viereck. Wie viele Möglichkeiten N gibt es, unter den n Ecken eines n-Ecks vier auszuwählen?
Für die Wahl der ersten Ecke stehen alle n Ecken zur Verfügung. Für die zweite Ecke hat man danach nur noch n − 1 Ecken zur Auswahl, da die zuerst ausgesuchte Ecke nicht mehr frei ist. Für die dritte und vierte Ecke kann man nur unter n − 2 und n − 3 Ecken wählen. Insgesamt gibt es also n(n – 1)(n – 2)(n – 3) Wahlmöglichkeiten für die vier Ecken.
Trotzdem ist dies noch nicht die gesuchte Anzahl von Kombinationen. Vier verschiedene Ecken können auf vierundzwanzig verschiedene Weisen aufgereiht werden. Diese jeweils vierundzwanzig Varianten sind bei den Wahlmöglichkeiten mitgezählt worden. Da aber für unser Problem die Reihenfolge der Ecken keine Rolle spielt, können wir die jeweils vierundzwanzig Varianten alle als gleich ansehen. Somit gibt es nur N = n(n – 1)(n – 2)(n – 3)/24 mögliche Kombinationen von vier Eckpunkten und somit auch höchstens so viele Schnittpunkte von Diagonalen. Diese Höchstzahl von Schnittpunkten kann auch tatsächlich erreicht werden.
Schreiben Sie uns!
Beitrag schreiben