Man kann ohne Weiteres eine Karte zeichnen, auf der jeder von Frankfurt ausgehende Großkreis als Strahl in der naturgetreuen Richtung erscheint. Die Entfernungen auf diesen Speichen muss man dann aber so ungleichmäßig auftragen, dass jedes hinreichend kleine Quadrat der Erdoberfläche wieder als ein (mehr oder weniger stark verkleinertes) Quadrat auf der Karte erscheint.

Erstaunlicherweise ist die so entstehende winkeltreue Azimutalkarte als Zentralprojektion von einem passend gewählten Punkt des Globus auf eine den Globus in einem Punkt (nämlich Frankfurt) berührende Kartenebene zu bekommen. Wo ist dieser Punkt?

Die winkeltreue Azimutalkarte wird in der Kartografie (wenig selbsterklärend, um das Mindeste zu sagen) als "stereografisch" gezeichnet.

Das gesuchte Projektionszentrum ist einfach der Punkt der Globusoberfläche, der Frankfurt diametral gegenüber liegt.

Im folgenden Bild sei b die Seite eines nahezu quadratischen Stücks der Erdoberfläche, das viel kleiner ist als gezeichnet und rechtwinklig aus der Zeichnung herausragt. Alle getönten Dreiecke sind (im Grenzfall, dass b verschwindend klein ist) zueinander ähnlich, wie man leicht überlegen kann. Daraus folgt, dass d nicht nur die Breite, sondern auch die Länge des Rechtecks ist, als welches das Quadrat auf der Karte abgebildet wird. Allgemein bleibt für jedes "sehr kleine" Rechteck oder Quadrat das Bild ähnlich (im geometrischen Sinn) zum Original. Damit ist die Abbildung konform, also infinitesimal verzerrungsfrei und winkeltreu. Der Maßstab ist natürlich von innen nach außen stark zunehmend.

Die Formeln für die neuen Koordinaten \(x\) und \(y\) in Abhängigkeit von geografischer Länge \(\lambda\), geografischer Breite \(\beta\) und Erdradius \(R\) sehen so aus:

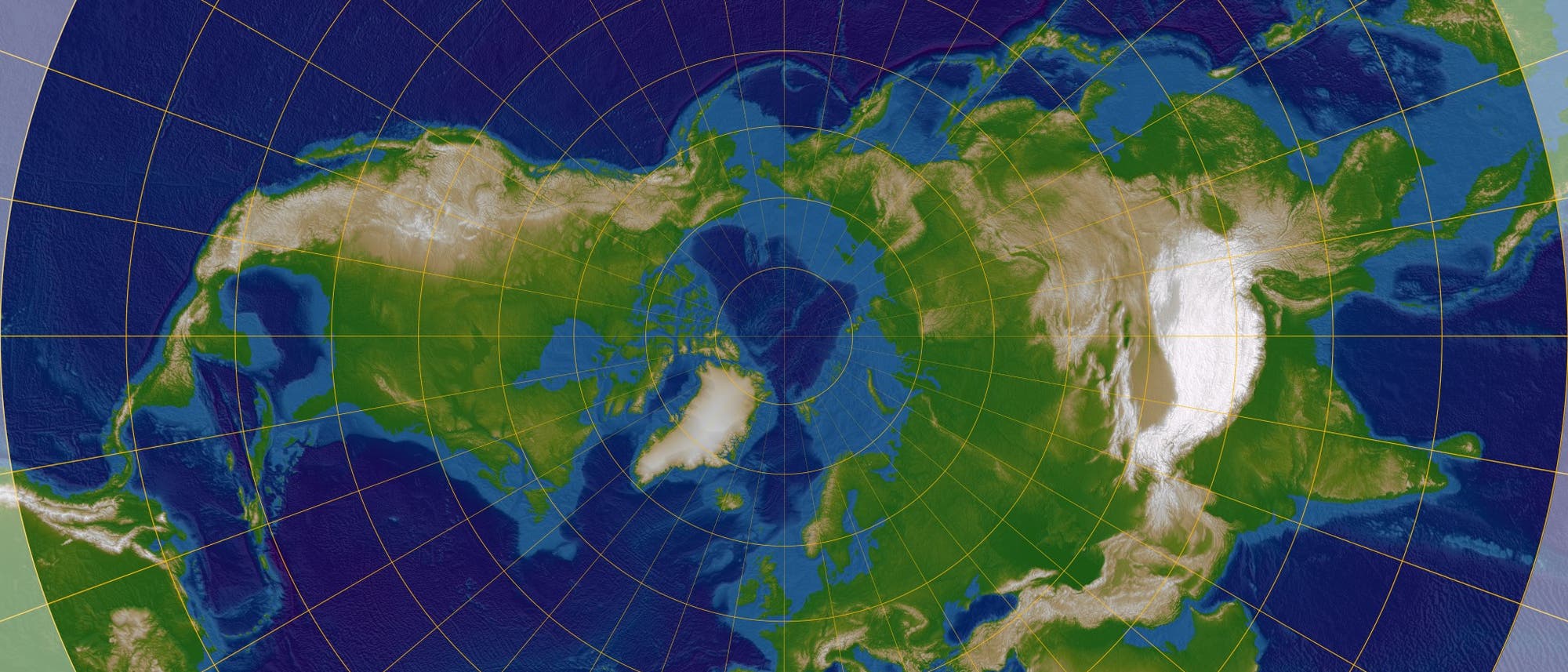
Ist der Nordpol der Berührpunkt von Globus und Erdkarte, bekommen wir dieses Bild mit speichenförmig angeordneten Meridianen und konzentrischen Breitenkreisen, die in diesem Fall zugleich Ringe für die Entfernungen vom Nordpol mit gleichen Stufen sind.

Die Karte ist "im Kleinen" verzerrungsfrei, also konform und winkeltreu, aber der Maßstab gleitet nach außen ins Unendliche, wir sehen also auf jeder endlichen Karte nur einen Teil der Erde (was aber durchaus mehr als die Hälfte sein kann):

Die Speichenellipsen (Tissot-Indikatrizen) sind stark vergrößerte Bilder von kleinen Kreisscheiben, die man sich auf dem Erdboden liegend vorstellen soll. Sie geben ein Maß für die Verzerrung in einer Karte an. In der stereografischen Karte werden die Speichenellipsen in alle Richtungen gleichermaßen vergrößert, bleiben also Kreise.

Ein Fußball sieht dabei so aus:

Eine Loxodrome (Weg mit konstantem Kurswinkel gegen die Meridiane) erscheint als logarithmische Spirale (denn das ist genau die Kurve mit der entsprechenden Eigenschaft in der Ebene):

Nun widmen wir uns aber mehr der Kundschaft aus der Umgebung von Frankfurt:

Alle Flugrouten von Frankfurt aus (also von der Kartenmitte bzw. dem Berührpunkt von Karte und Globus bei der Projektion) sehen wir hier als Geraden, alle anderen Luftlinien sehen wir als Kreisbögen, denn die Karte ist (was hier nicht bewiesen worden ist) kreistreu: Kreise auf der Kugel werden als Kreise oder Geraden der ebenen Karte abgebildet.

Die Entfernungen haben aber keinen gemeinsamen Maßstab. Immerhin kann man für die Entfernungen von Frankfurt aus ein passend beziffertes Lineal mit gleitendem (von innen nach außen anwachsendem) Maßstab verwenden.

Auch als Sternkarte ist die stereografische Abbildung nützlich: Man bekommt die Sternbilder verzerrungsfrei, wenn sie nicht zu groß sind, und muss nur auf die Umgebung von einem der beiden Himmelspole verzichten (oder auf die von sonst einer Himmelsgegend):

Die blauen Buchstaben sind Kurznamen der Sternbilder, die Monate bezeichnen den Lauf der Sonne am Fixsternhimmel. Drehbare Sternkarten (die modernen Nachfolger der Astrolabien) sind manchmal stereografische Azimutalkarten, oft aber auch Varianten mit weniger stark gleitendem Radialmaßstab und dann ohne Winkeltreue.