Ein ganz besonderes Viereck
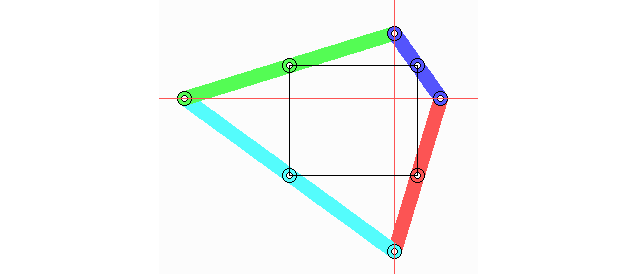
In diesem schönen ebenen Viereck aus Gelenkstangen der Längen 4 (blau), 8 (rot), 11 (grün) und 13 (türkis) Einheiten mit Löchern in den Seitenmitten liegen die Diagonalen rechtwinklig zueinander, und die Seitenmitten bilden ein Rechteck. Was wird davon bleiben, wenn die Freiheit genutzt wird, die die Gelenke bieten?
Der Winkel zwischen den Diagonalen bleibt bei 90o, und das Seitenmittenviereck bleibt somit ein Rechteck, dessen Seitenlängen sich aber ändern. In einem allgemeinen Viereck müsste das Seitenmittenviereck (nach dem Satz von Varignon) nur ein Parallelogramm bleiben, aber unser Viereck ist eben ein besonderes. Welche Beziehung gilt zwischen seinen Seitenlängen, und warum bedingen rechtwinklige Diagonalen ein Rechteck?
Geben Sie dazu den Abschnitten der Diagonalen von ihrem Schnittpunkt aus Namen und berechnen Sie daraus die Seitenlängen \(a, b, c\) und \(d\) des Vierecks. Sie finden dann \(a^2+c^2=b^2+d^2\), was ja auch für die Zahlen 4, 11, 13 und 8 (in dieser Reihenfolge) zutrifft, denn 16 + 169 = 121 + 64 = 185.
Wir haben also den Satz: Ein ebenes Viereck, bei dem die Quadrate der Gegenseiten die gleichen Summen haben, liegen die Diagonalen rechtwinklig zueinander, und die Seitenmitten bilden ein Rechteck.
Ist das auch umkehrbar?
Ja. Zum Beweis geben wir den Ecken die Koordinaten \(A = (0,0), B = (p,0)\), \(C = (q,r)\) und \(D = (s,t) \) und setzen sie in die Beziehung ein. Nach Ausmultiplizieren und Wegstreichen finden wir \(sq + rt = pq\) und damit \( \frac{r/q}{t/(s-p)} = -1\). Das Produkt der Steigungen der Diagonalen ist aber ebenfalls \( \frac{r/q}{t/(s-p)}\), und damit sind sie rechtwinklig zueinander. Da man jedes Viereck entlang jeder Diagonale in zwei Dreiecke teilen kann und darin die dazu parallele Mittelparallele als Verbindung von Seitenmitten findet, hat jedes (!) Viereck (das nicht einmal eben sein muss) als Seitenmittenviereck ein Parallelogramm (Satz von Varignon), im Fall zueinander rechtwinkliger Diagonalen also ein Rechteck.
Wenn wir einen Metallbaukasten benutzen, haben wir einen besonderen Grund für die Frage: Gibt es außer dem gegebenen Beispiel auch noch andere ganzzahlige Seitenverhältnisse?
Ja. Die Tabelle zeigt die Summe der Quadrate aus der Zeilen- und der Spaltenzahl. Die Matrix ist symmetrisch, das heißt in Zeile \(n\) und Spalte \(m\) steht dieselbe Zahl wie in Zeile \(m\) und Spalte \(n\). Zahlen, die über diese – triviale – Übereinstimmung hinaus mehrfach vorkommen, sind rot geschrieben. Es gibt also eine gewisse Auswahl ganzzahliger Werte. Sehr kurze Seiten sind allerdings nicht besonders eindrucksvoll, da das Viereck dann fast wie ein Dreieck aussieht.
Wie bereits im Rätsel "Varignon" erwähnt, gilt der Satz von Varignon auch für ein nicht-ebenes Viereck. Gilt unser Satz über die rechten Winkel und die Quadratsummen ebenfalls in drei Dimensionen, also auch für ein Viereck, das aus 4 der 6 Kanten eines (im Allgemeinen unregelmäßigen) Tetraeders gebildet wird?
Denken wir uns das bisherige Bild des Vierecks als Projektion eines Tetraeders, bei dem eine Diagonale in der Zeichenebene liegt, die andere aber in einer Höhe \(h\) darüber. Die beiden Diagonalen bilden nun zwei zueinander rechtwinklige Kanten des Tetraeders. Die anderen vier Kanten werden durch die bisher als Viereckseiten gedeuteten Linien in verkürzender Parallelperspektive gezeigt. Das ändert aber nichts daran, dass die Summen ihrer Quadrate immer noch überkreuz gleich sind, denn nach Pythagoras kommt zu jedem Seitenquadrat nun \(h^2\) hinzu.
Auf halber Höhe ist die Schnittfläche des Tetraeders unser Rechteck, von dem es halbiert wird. In jeder anderen Höhe ist die Schnittfläche ein Rechteck mit anderem Seitenverhältnis (aber mit gleichem Umfang). Haben die Diagonalen unseres Rechtecks die Länge \(L\), so haben die beiden Bimediane, deren Bilder diese Diagonalen sind, die Länge \(L^2 + h^2\). Die Rechtwinkligkeit von zwei sich gegenüber liegenden Kanten zieht beim Tetraeder also einige Besonderheiten nach sich. Nathan Altshiller Court nennt solche Tetraeder "semi-orthocentric" und behandelt sie im "Monthly" im Mai 1953.
Schreiben Sie uns!
Beitrag schreiben