Hemmes mathematische Rätsel: Ein Vierfarbenproblem
Der Amerikaner Stephen Barr wuchs in England auf und zog als Achtzehnjähriger in die USA, die Heimat seiner Eltern. Dort begann er eine sehr erfolgreiche Karriere als Künstler, Designer und Autor. Obwohl seine Mathematikausbildung nie über den Schulunterricht hinausging, war er ein äußerst kreativer Erfinder mathematischer Rätsel. In den 1960er Jahren schrieb er drei Bücher mit den Titeln und Experiments in Topology (1964), A Miscellany of Puzzles: Mathematical and Otherwise (1965) und 2nd Miscellany of Puzzles: Mathematical and Otherwise (1969). Aus dem ersten Buch stammt folgendes Problem:
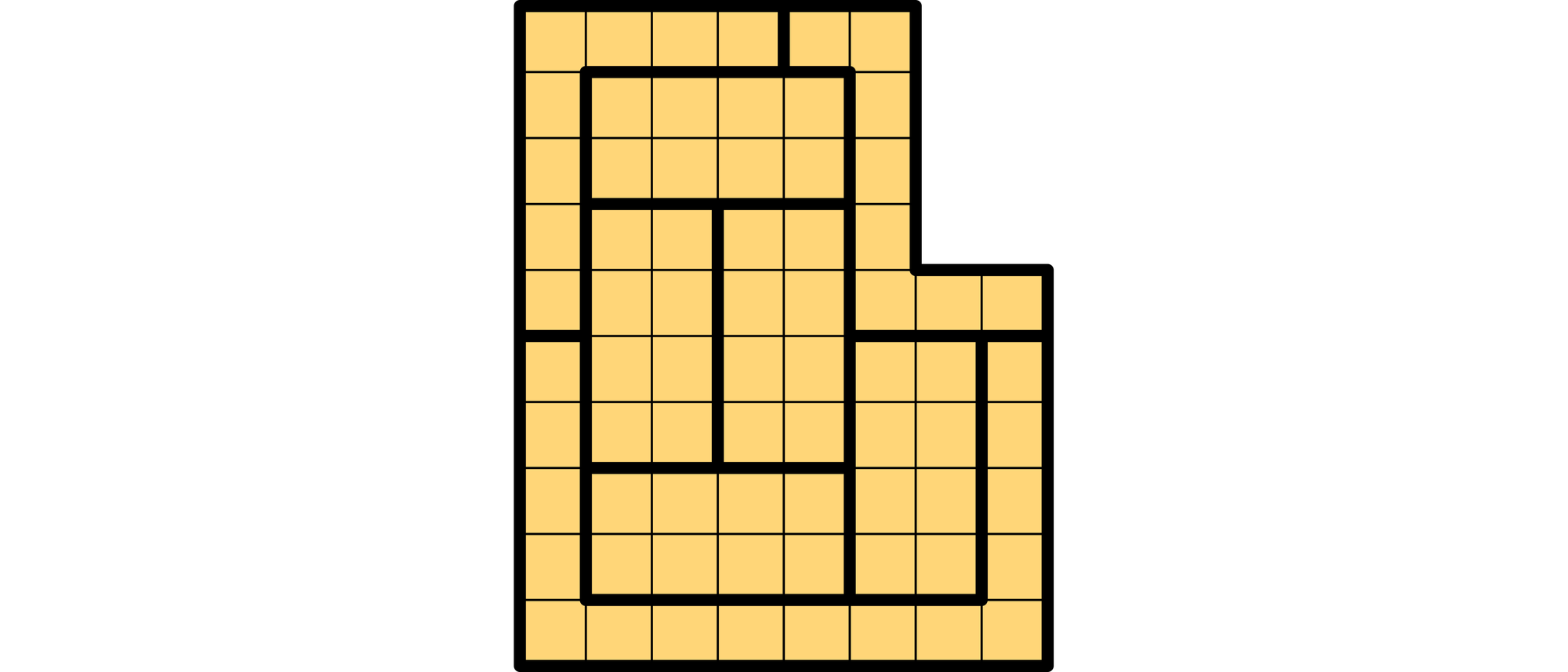
Eine große Hallenwand ist in acht Flächen unterteilt, die alle eine Größe von je 8 m2 haben, nur die U-förmige unterste Fläche ist 16 m2 groß. Die Flächen sollen so bunt angestrichen werden, das nirgendwo zwei gleichfarbige mit einer Seite aneinander stoßen. Innerhalb einer Fläche darf sich die Farbe nicht ändern.
1976 bewiesen Kenneth Appel und Wolfgang Haken, dass die Flächen einer Wand, ganz egal wie viele es sind und wie sie verschlungen sind, immer auf diese Weise mit höchstens vier Farben angestrichen werden kann. Aber stimmt dies auch noch, wenn die Farbmengen vorgegeben sind? Dem Maler stehen für seine Arbeit nämlich rote Farbe für 24 m2, gelbe Farbe für 24 m2, grüne Farbe für 16 m2 und blaue Farbe für 8 m2 zur Verfügung. Wie muss er die Flächen streichen? Ist das Problem überhaupt lösbar, und wenn nicht, warum nicht?
Streicht man die Felder 4, 5 und 8 mit den Farben A, B und C an, muss das Feld 7 entweder mit der Farbe D oder der Farbe A gestrichen werden. Im ersten Fall ergeben sich daraus zwei verschiedene mögliche Färbungen der Wand, die sich nur dadurch unterscheiden, dass die Felder 1 und 3 entweder mit D und C oder mit C und D gestrichen werden. Der zweite Fall hingegen führt zu einer eindeutigen Färbung der Wand.
Bei allen drei möglichen Färbungen müssen mit jeder Farbe jeweils zwei Felder gestrichen werden. Blaue Farbe steht dem Maler jedoch nur für 8 m2 und somit höchstens für ein Feld zur Verfügung. Deshalb kippt er die blaue Farbe und ein Drittel der roten Farbe zusammen und verrührt sie. Dadurch erhält er violette Farbe für 16 m2. Nun hat der Maler mehrere Möglichkeiten, wie er die Wand streichen kann. Die Abbildung zeigt eine davon.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.