Hemmes mathematische Rätsel: Feynmans Divisionsrätsel
Der Physiker Richard P. Feyman wurde 1918 in Queens geboren und starb 1988 in Los Angeles. Er war einer der ganz großen Physiker des 20. Jahrhunderts und hat wesentliche Beiträge zum Verständnis der Quantenfeldtheorien geliefert. Zusammen mit Shin'ichiro Tomonaga und Julian Schwinger erhielt er 1965 den Nobelpreis für Physik für seine Arbeit zur Quantenelektrodynamik. Seine anschauliche Darstellung quantenfeldtheoretischer elementarer Wechselwirkungen durch Feynman-Diagramme ist heute ein Standard. Für Feynman war es immer wichtig, die Physik den Laien verständlich zu machen. Sein Charisma und die Fähigkeit, auf seine Zuhörer einzugehen, ließen seine Vorlesungen und Vorträge legendär werden.
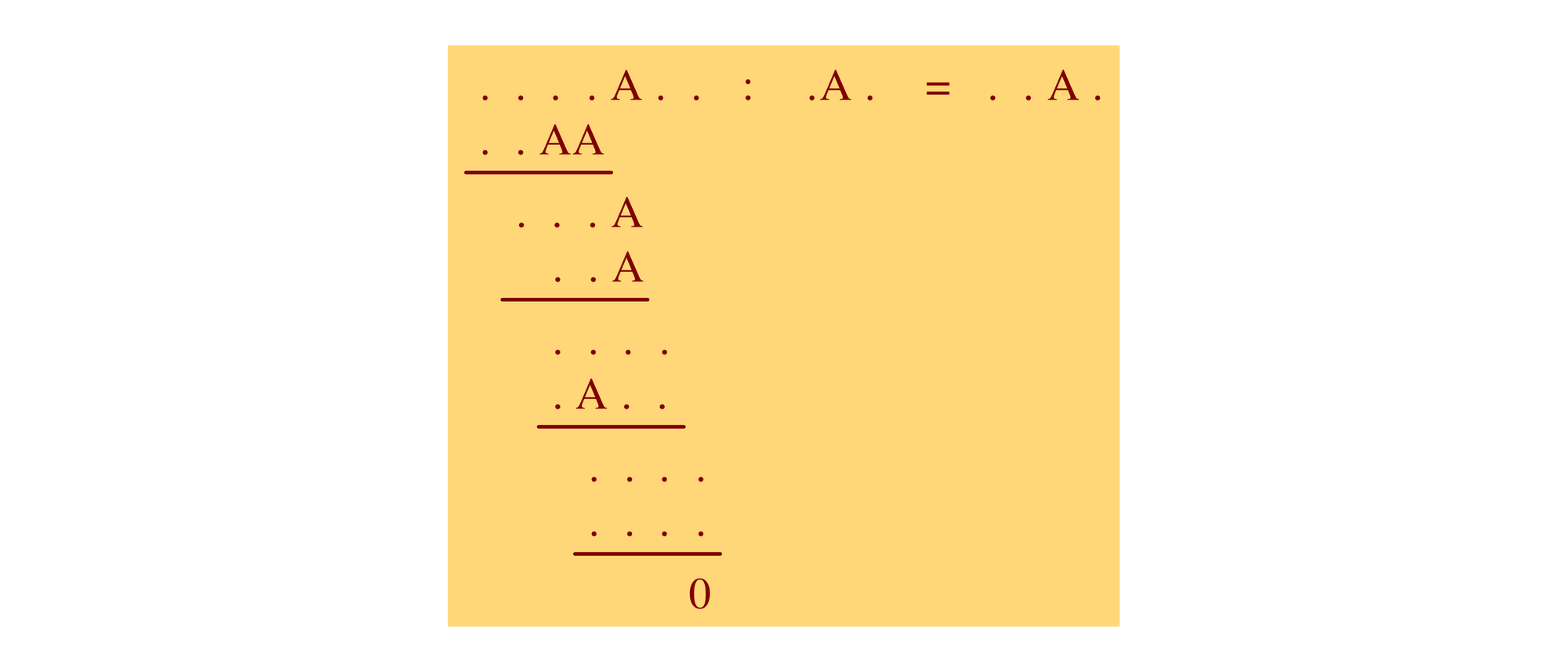
Im November 1939, als Feynman Student an der Princeton University war, bat er in einem Brief an seine Mutter, ein beigelegtes Rätsel an seinen Vater weiterzugeben. Dieses Rätsel war eine schriftliche Division, bei der er jede Ziffer bis auf eine durch einen Punkt oder durch ein A ersetzt hatte. Sein Vater sollte die Rechnung rekonstruieren. Er schrieb dazu: Eine der zehn Ziffern habe ich überall durch ein A ersetzt, alle anderen Ziffern durch einen Punkt. Keiner der Punkte steht also für die Ziffer, die das A darstellt.
Wir nennen die durch Punkte ersetzten Ziffern des Divisors und des Quotienten b, c, d, e und f, von denen keine gleich A sein darf.

Aus der zweiten und vierten Zeile folgt, dass das Produkt d · bAc auf AA endet und das Produkt e · bAc auf A. Da das erste Produkt vierstellig, das zweite aber nur dreistellig ist, muss d > e sein. Es müssen also d · c und e · c auf A enden, wobei weder d = c oder e = c sein darf. Probiert man für c, d und e alle Ziffernkombinationen durch, stellt man fest, dass nur die Kombination c = 4, d = 7 und e = 2 in Frage kommt und zu A = 8 führt.

Aus der sechsten Zeile folgt, das Produkt 8 · b84 ist vierstellig und hat eine 8 als Hunderterstelle. Da 8 · 84 = 672 ist und somit schon 6 zur Hunderterstelle beiträgt, muss die Endziffer von 8 · b noch die fehlende 2 liefern. Das ist nur bei b = 4 oder b = 9 möglich. Die 9 scheidet aber aus, weil sonst die vierte Zeile vierstellig wäre. Folglich ist b = 4. Zum Schluss überprüft man noch für die neun möglichen Werte für f, ob die drittletzte Stelle des Produkts 484 · 728f eine 8 ist. Dies ist nur für f = 9 der Fall. Damit ist das Problem vollständig gelöst.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.