Hemmes mathematische Rätsel: Fliege und Spinne
Henry Ernest Dudeney war wohl der bedeutendste Rätselerfinder, der jemals lebte. Er wurde 1857 in Mayfield in England geboren und besuchte niemals eine Universität, sondern erwarb seine Mathematikkenntnisse autodidaktisch. Dudeney entwarf über Jahrzehnte für zahlreiche Zeitungen und Magazine regelmäßig Denksportprobleme. Die meisten seiner Rätsel fasste er später auch zu Büchern zusammen. Er starb am 24. April 1930. Das folgende Problem veröffentlichte Dudeney 1905 in der Zeitung »Daily Mail«.
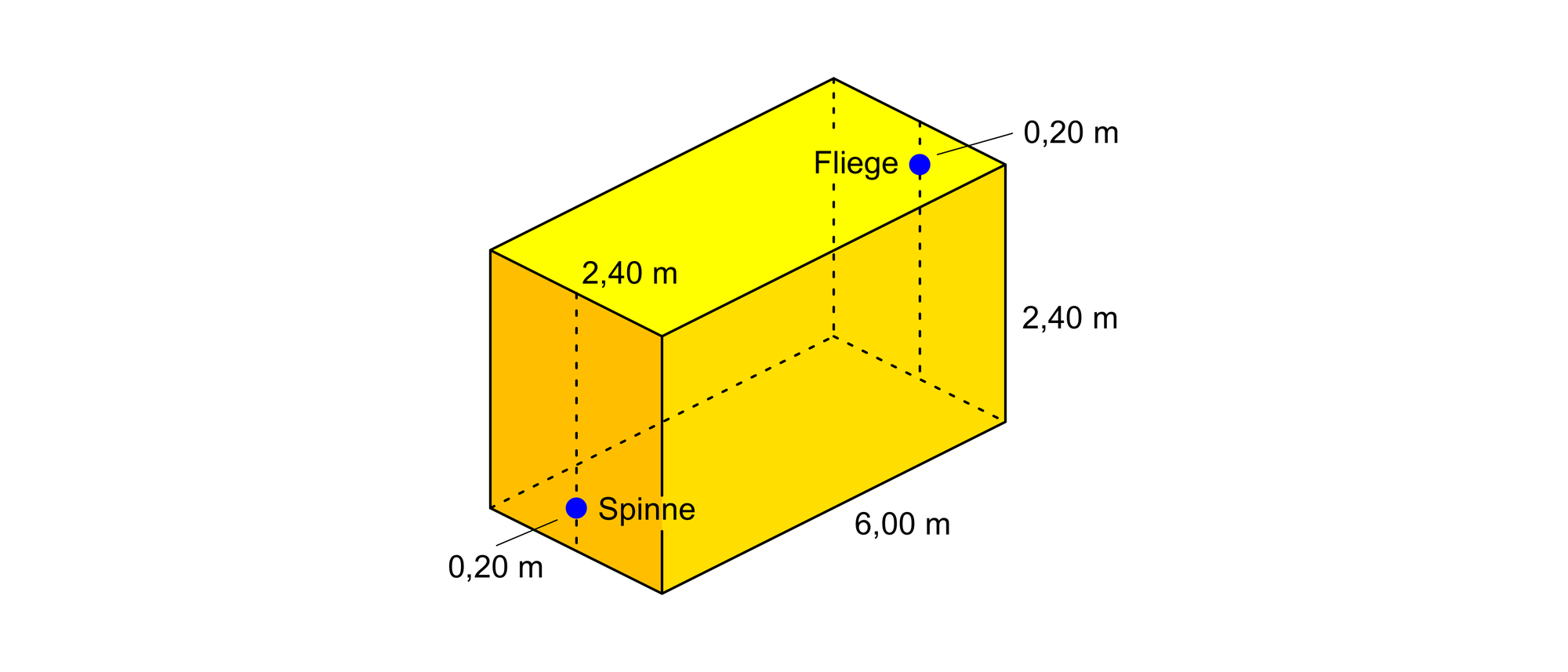
In einem Raum von 2,40 m × 6,00 m Grundfläche und mit 2,40 m hohen Wänden hockt auf der Mittellinie einer der beiden quadratischen Wände, 20 cm über dem Boden, eine Spinne. Auf der Mittellinie der gegenüberliegenden Wand, 20 cm unter der Decke, sitzt eine Fliege. Die Spinne möchte die Fliege fressen und krabbelt auf einem möglichst kurzen Weg zu ihr hin. Da die Spinne nicht fliegen kann, darf ihr Weg natürlich nur über die Wände, die Decke und den Fußboden gehen. Wie lang ist der Weg der Spinne?
Wir stellen uns den Raum als Pappschachtel vor, die wir entlang einiger Kanten aufschneiden und flach auf dem Tisch ausbreiten können. Die Wand, auf der die Fliege sitzt, lassen wir in dem Pappmodell dreimal vorkommen: Einmal ist sie am Boden befestigt, einmal an einer Seitenwand und einmal an der Decke. In diesem Modell gibt es drei direkte Wege, die die Spinne zur Fliege hin nehmen kann.
Würde man in dem Modell weitere Wände doppelt zeichnen, so gäbe es noch mehr direkte Wege. Sie liegen aber entweder symmetrisch zu den ersten drei Wegen, oder aber sie sind deutlich länger. Wir bezeichnen die 6,00 m langen Kanten mit a, die 2,40 m langen Kanten mit b und den Abstand von 20 cm, den die Spinne vom Boden und die Fliege von der Decke hat, mit c. Die drei Wege haben die Längen:
l1 = a + b = 8,40 m
l2 = √((a + b/2 + c)2 + (3b/2 − c)2) ≈ 8,14 m
l3 = √((a + 2c)2 + (2b)2) = 8,00 m
Der kürzeste Weg der Spinne bis zur Fliege verläuft also über drei Wände und über den Boden und die Decke des Raumes.
Schreiben Sie uns!
Beitrag schreiben