Leichter Ring
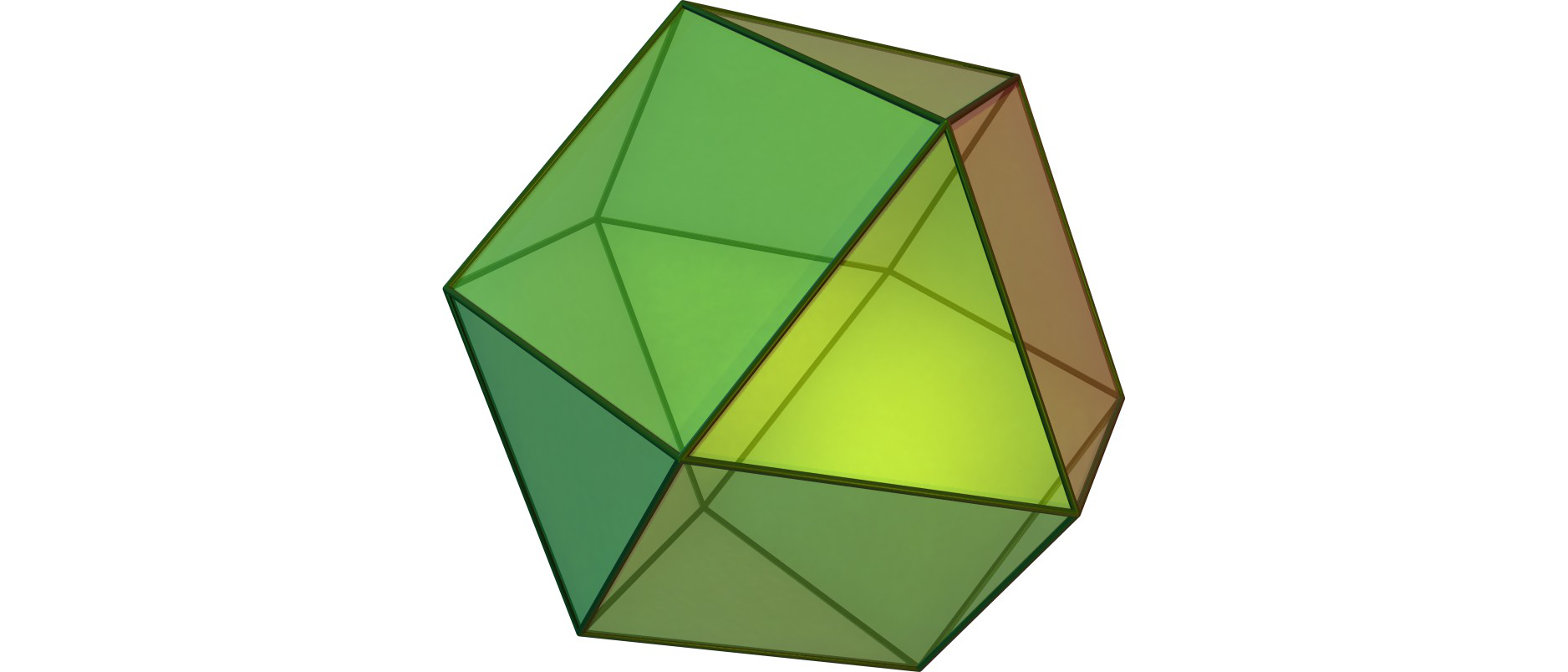
Aus welchem Polyeder kann man ein Kuboktaeder herausschneiden, so dass ein sehr volumenarmes Torus-Polyeder aus lauter regelmäßigen Vielecken bleibt?
Betrachten Sie die vierzählige Doppelkuppel aus acht gleichseitigen Dreiecken und zehn Quadraten, von denen dann Quadrate durch das Entfernen des Kuboktaeders entfallen.
Die vierzählige Kuppel besteht aus einem achteckigen "Boden", abwechselnd quadratischen und dreieckigen, nach innen geneigten "Seitenwänden" und einem quadratischen "Deckel". Die vierzählige Doppelkuppel besteht aus zwei Boden an Boden aneinandergelegten Kuppeln, und zwar so, dass Dreieck an Dreieck grenzt. Unter den Johnson-Polyedern hat sie die Nummer 28. Jetzt müssen Sie nur noch die beiden Deckel wegnehmen …
Dieses Torus-Polyeder findet sich in Bonnie Madison Stewarts Buch auf Seite 33. Die äußeren Kanten bilden eine vierzählige Doppelkuppel. Innenliegend befindet sich das Kuboktaeder.
Der Reiz dieses Körpers besteht wohlgemerkt darin, dass das innere und das äußere Polyeder ausschließlich aus regelmäßigen Polygonen gleicher Kantenlänge bestehen. Das topologische Geschlecht ist 1 (das Polyeder hat genau ein Loch). Die Euler-Charakteristik \(\chi\) lässt sich aus den 16 Ecken, 48 Kanten und 22 Flächen berechnen (die beiden quadratischen Fenster zählen nicht mit). Das Ergebnis ist \(\chi=0\), genau wie bei einem Torus.
Schreiben Sie uns!
Beitrag schreiben