Mitten der Umfangshalbierenden
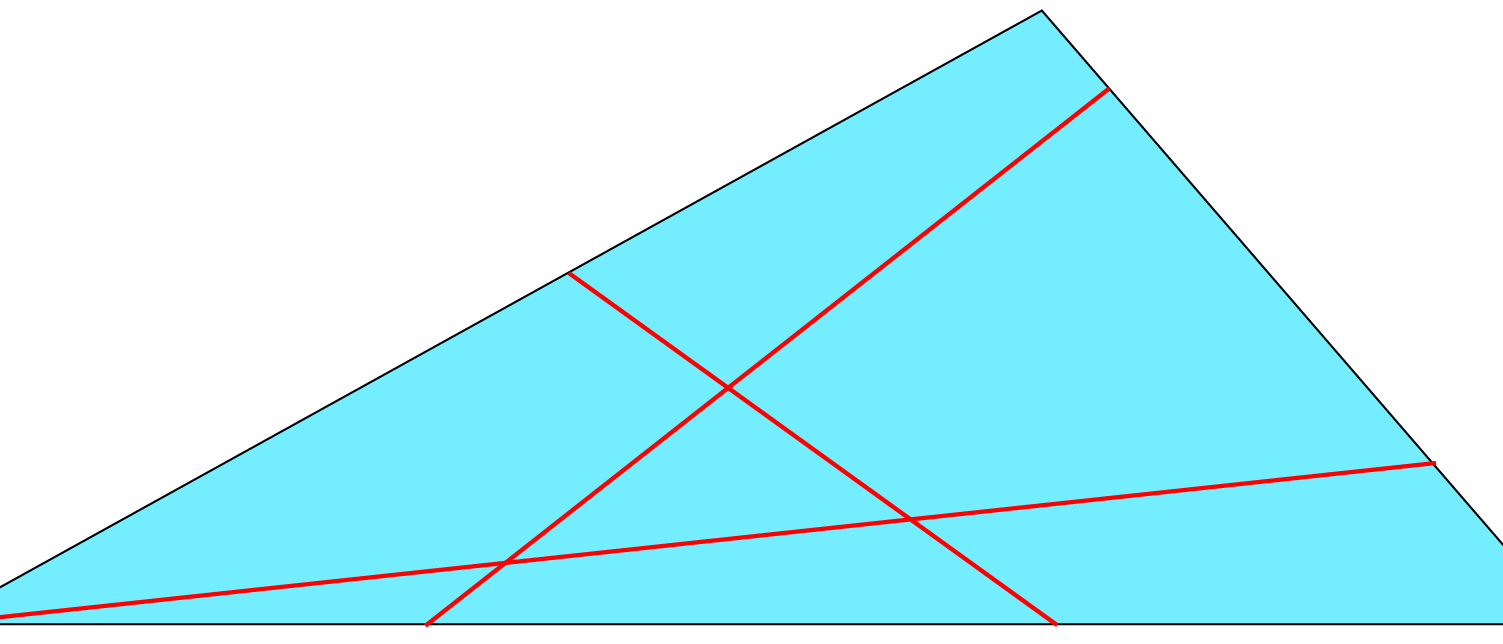
Eine Umfangshalbierende eines Dreiecks ist eine Strecke, die das Dreieck zerschneidet, und zwar so, dass beide Teile die Hälfte vom Umfang des Dreiecks abbekommen. Wo liegen die Mittelpunkte aller Umfangshalbierenden?
Nutzen sie folgende Eigenschaften von Dreiecken, um die Lösung zu konstruieren, und benutzen Sie auch das Dreieck aus den Seitenmitten.
Wandern zwei Punkte gleich schnell auf zwei Geraden, so wandert ihr Mittelpunkt auch auf einer Geraden (wie man besonders einfach mit Koordinaten einsieht).
Der Berührpunkt eines Ankreises eines Dreiecks halbiert den Umfang eines Dreiecks. Der Berührpunkt ist also gleich weit von der gegenüberliegenden Ecke entfernt, egal ob man rechts oder links herum die Entfernung entlang seiner Seiten misst. Warum? Die drei Dreiecksseiten sind Tangenten an den Ankreis. Die Strecken von einem Punkt (zum Beispiel einem Eckpunkt des Dreiecks) zum Berührpunkt seiner beiden Tangenten mit dem Kreis sind stets gleich lang.
Die Berührpunkte des Inkreises und des anliegenden Ankreises auf einer Dreiecksseite liegen symmetrisch zur Seitenmitte.
Die gesuchten Mitten liegen auf den Seiten des Dreiecks aus den Inkreisberührpunkten des kleinen blauen Seitenmittendreiecks.
1. Zunächst zeichnet man die Seitenmitten des schwarzen Dreiecks ein. Verbindet man diese, erhält man das blaue Seitenmittendreieck.
2. Das blaue Seitenmittendreieck unterteilt das ursprüngliche schwarze Dreieck in vier zueinander deckungsgleiche Dreiecke.
3. Als nächsten Schritt bildet man von den äußeren kleinen Dreiecken (mit jeweils zwei schwarzen und einer blauen Seite) den Ankreis an die blaue Seite und zeichnet den Berührpunkt von Ankreis und Seite ein.
4. Dieser Punkt halbiert (gemeinsam mit der fernen Ecke) den Umfang des jeweiligen kleinen äußeren Dreiecks und damit auch den des großen schwarzen Dreiecks (Streckung des kleinen Dreiecks mitsamt Umfangshalbierender mit dem Faktor 2). Damit hat man drei spezielle Umfangshalbierende des schwarzen Dreiecks gefunden, nämlich diejenigen, die durch die Ecken gehen.
5. Die beschriebenen Ankreisberührpunkte sind zugleich die Inkreisberührpunkte des blauen Seitenmittendreiecks; denn der Inkreisberührpunkt eines schwarz-blau-schwarzen Dreiecks liegt symmetrisch zu dessen Ankreisberührpunkt. Also fällt er auf diesen Ankreisberührpunkt, wenn man das schwarz-blau-schwarze Dreieck durch Halbdrehung um die blaue Seite mit dem blauen Dreieck zur Deckung bringt.
6. Für die Punkte, die sozusagen auf den Seiten des großen schwarzen Dreiecks wandern, wandert der Halbierungspunkt auf jeweils einer anderen Seite mit dem gleichen Tempo mit. Der Halbierungspunkt wandert daher auf einer Seite des grünen Dreiecks aus den soeben gefundenen drei Punkten.
Die Aufgabe mit der bemerkenswerten Aussage (wer denkt schon, dass ein geometrischer Ort der Umfang eines Dreiecks ist?) habe ich in Honsberger ("More morsels") als Nr. 50 gefunden.
Schreiben Sie uns!
Beitrag schreiben