Polygon-Schwerpunkte
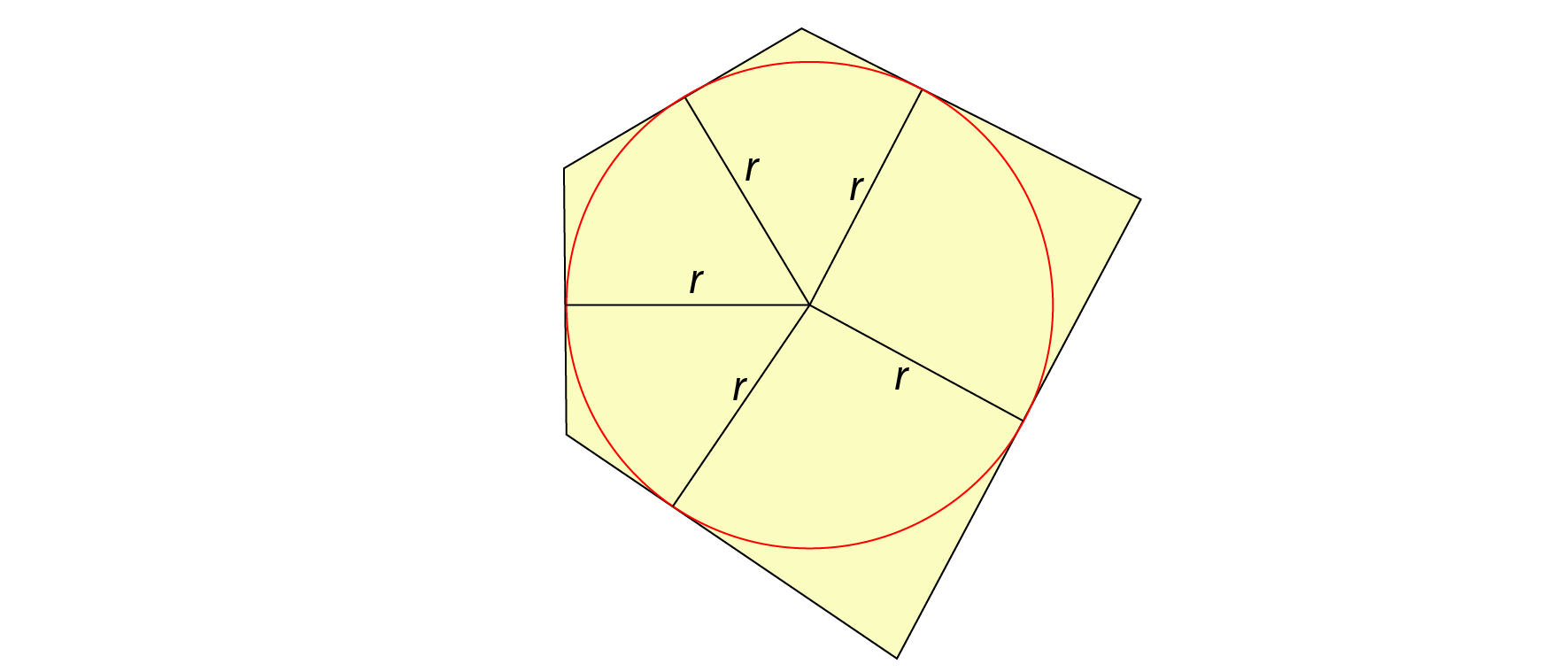
Stellen Sie sich ein ebenes Polygon aus Blech und dasselbe aus Draht vor. Das Vieleck habe einen Inkreis, das heißt, dass dessen Seiten Tangenten eines Kreises sind.
In diesem Fall liegt der Schwerpunkt der Fläche (Blech-Polygon) auf der Strecke zwischen dem Inkreismittelpunkt und dem gemeinsamen Schwerpunkt der Seiten (Draht-Polygon). Der Flächenschwerpunkt teilt diese Strecke im Verhältnis 2/3 zu 1/3. Wieso?Wo liegen der Schwerpunkt einer Dreiecksfläche und der einer Seite des Dreiecks? Zerlegen Sie das Polygon geschickt.
Wir zerlegen das Polygon in Dreiecke mit den Polygon-Seiten als Grundseiten und dem Inkreismittelpunkt als Spitzen. Da sie alle gleich lange Höhen zu diesen Grundseiten haben, verhalten sich ihre Flächen wie die Längen ihrer Grundseiten. Damit haben auch deren Massen das Verhältnis der jeweiligen Grundseiten, falls diese aus Draht sind.
Der Schwerpunkte einer Grundseiten eines Dreiecks ist dessen Mittelpunkt. Der Schwerpunkt einer Dreiecksfläche ist der Schnittpunkt der Seitenhalbierenden \(S_a\), \(S_b\), und \(S_c\). Der Flächenschwerpunkt eines Dreiecks teilt die Seitenhalbierenden im Verhältnis 2:3.
Die Flächen haben nun irgendwo einen gemeinsamen Schwerpunkt, und die Grundseiten auch. Von der Inkreismitte aus liegen sie im Verhältnis 2:3 verschieden weit entfernt in einer gemeinsamen Richtung.
In drei Dimensionen gilt das Entsprechende mit dem analogen Beweis: Hat ein Polyeder eine Inkugel, so liegt der Schwerpunkt des Volumens 3/4-mal so weit entfernt vom Inkugelmittelpunkt wie der der Oberfläche. Beide liegen aber in der gleichen Richtung. Insbesondere liegt der Volumen-Schwerpunkt einer Pyramide in 1/4 der Höhe.
Schreiben Sie uns!
Beitrag schreiben