Steiner-Kette
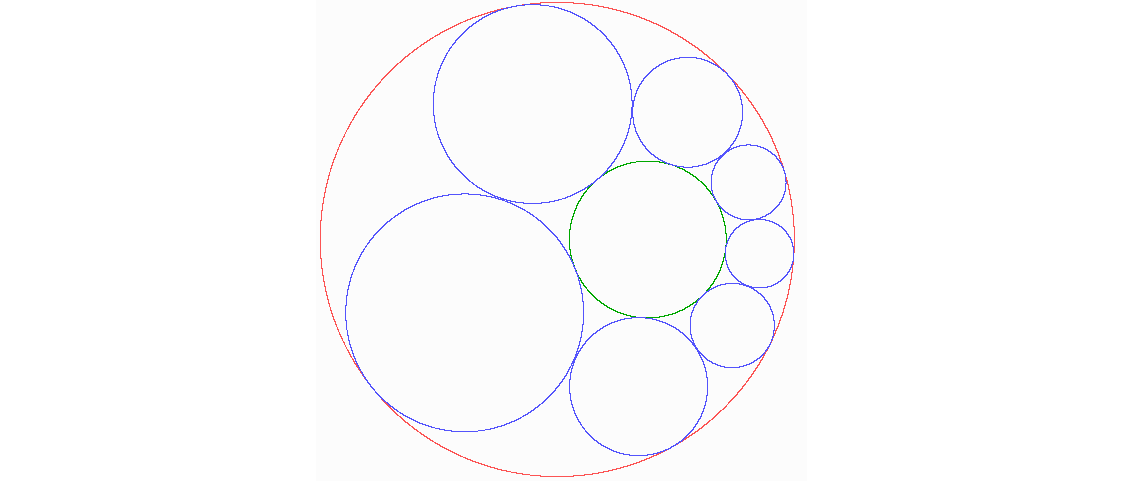
Das Bild zeigt einen roten und einen grünen Kreis und dazwischen sieben blaue Kreise, deren jeder den roten, den grünen und seine beiden blauen Nachbarkreise berührt.
Denken Sie sich nun den roten und den grünen festgehalten, ohne die blauen Kreise. Nun setzen Sie einen (von den blauen Kreisen unterschiedlichen!) Kreis zwischen den roten und den grünen, der beide wieder paarweise berührt. Kann man dann die Kette so fortsetzen, dass sie sich wie die blaue Kreiskette ohne Lücke und ohne Überlappung schließt?
Denken Die an die Inversion am Kreis: Dabei wird der Punkt mit den Polarkoordinaten \((r,\omega)\) auf den Punkt mit \(\left(\frac{R^2}{r},\omega\right)\) abgebildet, wenn der Inversionkreis den Mittelpunkt in \((0,0)\) und den Radius \(R\) hat. Wir benutzen nun die Tatsache, dass die Inversion Kreise auf Kreise abbildet, wobei Geraden als Grenzfälle zu den Kreisen gezählt werden.
So unglaublich es klingt: Es funktioniert:
Aber wie kann man erklären?
Dass man Kreisketten mit gleich großen Kreisen zwischen konzentrische Kreise mit passenden Radien setzen und dann drehen kann, ist klar. Genauer: Man gibt sich eine Anzahl \(n\) von Kreisen vor, die man von innen in den Außenkreis setzt, und wählt deren Radius so, dass sie sich gegenseitig berühren. Dann wählt man den Radius des Innenkreises so, dass er alle Kettenkreise berührt. Also gibt es für jedes \(n>2\) genau ein passendes Radienverhältnis zwischen den zwei konzentrischen Kreisen. Dann rollt der Innenkreis an den Kettenkreisen und diese am Außenkreis ab – das Prinzip des Kugellagers. Nur sollten bei letzterem die Kettenkreise einander besser nicht berühren.
Die Inversion am Kreis bildet alle Punkte eines Kreises auf die Punkte eines anderen Kreises ab – oder einer Geraden, wenn der erste Kreis durch den Mittelpunkt des Inversionskreises geht. Bei uns ist \(n = 7\), der Inversionskreis ist in der unteren Animation schwarz gekennzeichnet, und seine Mitte ist als Kreuzchen markiert.
In der Animation liegen zwei kleine konzentrische Kreise (rot und grün) innerhalb des schwarzen Inversionskreises. Und zwar ist der rote Kreis kleiner als der grüne. Wie oben beschrieben, passen sieben gleiche kleine blaue Kreise zwischen den roten und den grünen Kreis. Nun wendet man die Inversion am schwarzen Kreis auf alle Punkte der kleinen Kreise an; dabei geraten die Bildpunkte in den Außenbereich des schwarzes Kreises. (Eine Inversion bildet stets das Innere des Inversionskreises auf das Äußere ab und umgekehrt.) Gemeinsame Punkte mehrerer Kreise – hier Berührpunkte, sonst auch Schnittpunkte – werden wieder auf solche abgebildet, allerdings wird der Mittelpunkt eines Kreises nicht auf den Mittelpunkt seines Bildkreises abgebildet. Darum sind der rote und der grüne Kreis auch nicht mehr konzentrisch, die Berührpunkte der insgesamt neun Kreise bleiben aber bestehen.
Nach einer Inversion müssen die beiden festen und vorher konzentrischen (roten und grünen) Kreise nicht unbedingt ineinander liegen:
Eine etwas andere Erklärung kann man mit der stereografischen Projektion geben. Man stelle sich eine punktförmige Lichtquelle am Nordpol einer (im Prinzip transparenten) Erdkugel vor, die ihrerseits mit dem Südpol auf einer Ebene (sagen wir dem Tisch) liegt. Die stereografische Projektion bildet alle Kreise der Kugeloberfläche auf Kreise oder Geraden der Tischebene ab. Man lege nun eine Kette gleich großer Kreise um den Äquator, so dass ihre Berührpunkte ebenfalls auf dem Äquator liegen, dazu die beiden Breitenkreise, die die Kette im Norden und im Süden berühren. Projiziert man nun dieses Ensemble vom Nordpol der Kugel aus auf die Tischebene, so bekommt man die Kette gleich großer Kreise zwischen einem kleinen und einem großen Kreis. Rollt man die Kugel ein wenig auf dem Tisch, lässt aber die Lichtquelle am obersten Punkt der Kugel, so ändern sich die Größen der Kreise, aber nicht ihre Formen und die Zahl ihrer Berührpunkte.
Die Steiner-Kette ist benannt nach dem Schweizer Mathematiker Jakob Steiner (1796–1863), der sie definierte und ihre wesentlichen Eigenschaften beschrieb.
Schreiben Sie uns!
Beitrag schreiben