Tangentenabschnitte
© Norbert Treitz (Ausschnitt)
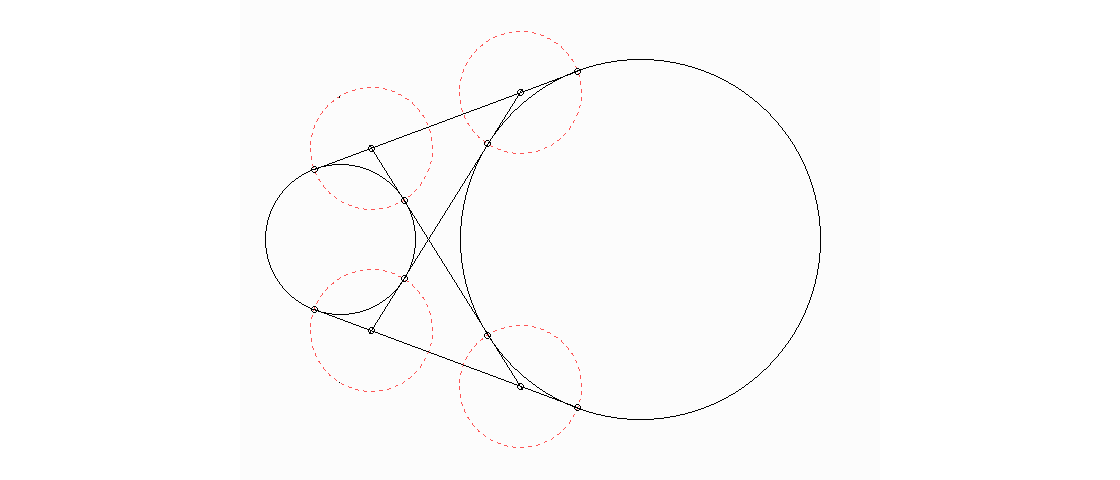
Warum sind alle 4 gestrichelten Kreise gleich groß?
Betrachten Sie die Symmetrie von zwei sich schneidenden Tangentenabschnitten an einem Kreis.
© Norbert Treitz (Ausschnitt)
Die Strecken zwischen je zwei Berühr- oder Schnittpunkten (bzw. deren Längen) sind hier mit a, b, c, und d bezeichnet. Über die Klappsymmetrie der ganzen Figur müssen wir ja wohl nicht lange reden. Was wirklich verblüfft, ist die Gleichheit von a und b, die noch zu zeigen ist.
Zwei Tangentenabschnitte von einem bestimmten Punkt an den kleineren Kreis sind gleich, nämlich
a + c = b + d
Ebenso finden wir für den großen:
b + c = a + d
Ziehen wir die Gleichungen voneinander ab, gibt das a – b = b – a, also die Behauptung a = b.
Schreiben Sie uns!
Beitrag schreiben