Hemmes mathematische Rätsel: Trapeze im Dreieck
Der spanische Mathematikprofessor Claudio Alsina und amerikanische Mathematiklehrer Roger B. Nelsen veröffentlichten 2010 in den USA ein Buch mit dem Titel »Charming Proofs: A Journey Into Elegant Mathematics«. Aus dieser wunderschönen Sammlung eleganter mathematischer Beweise und kniffliger Probleme stammt das heutige Rätsel.
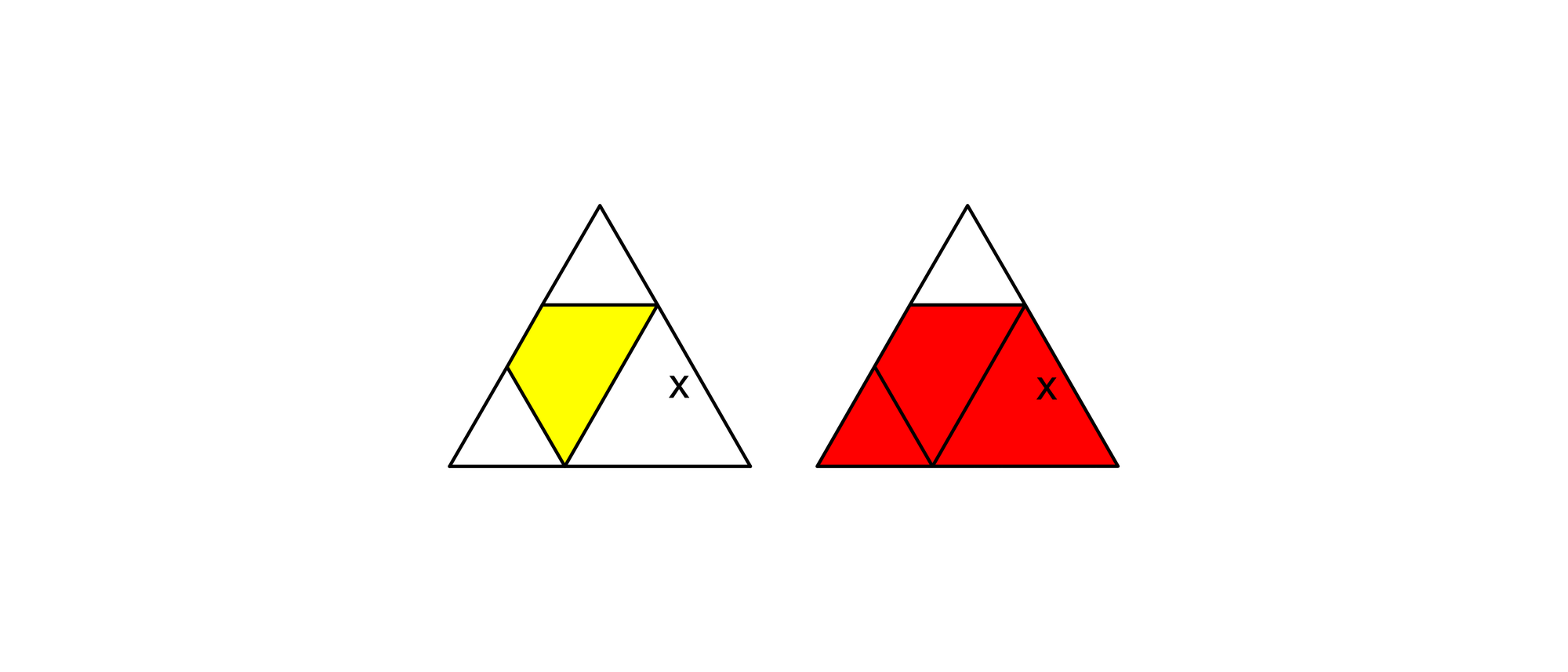
Ein gleichseitiges Dreieck der Seitenlänge eins wird in drei Dreiecke und das gelbe Trapez unterteilt. Dazu zeichnet man drei Strecken in die Figur ein, die jeweils zu einer Dreiecksseite parallel sind. Zwei der kleinen Dreiecke und das kleine Trapez bilden zusammen das rote Trapez. Wie groß muss x sein, damit das gelbe und das rote Trapez ähnlich sind, also die gleichen Proportionen haben?
Die einander entsprechenden Innenwinkel der beiden Trapeze sind gleich und entweder 60 oder 120 Grad. Darum braucht man für die Ähnlichkeit nur noch den Wert für x zu finden, bei dem die Verhältnisse einander entsprechender Seitenlängen bei beiden Trapezen auch gleich sind.
Das äußere Dreieck hat die Seitenlänge eins und das große innere die Seitenlänge x. Daraus kann man leicht die Längen aller anderen Strecken der Figur ermitteln. Damit die beiden Trapeze ähnlich sind, müssen das Längenverhältnis der kurzen Grundseiten und das der Schenkel gleich sein. Das bedeutet (2x – 1)/(1 – x) = (1 – x)/x.
Dieser Ausdruck lässt sich zu der quadratischen Gleichung x2 + x – 1 = 0 umformen, die als positive Lösung x = 1⁄2(√5 – 1) ≈ 0,618 hat. Dies ist der Kehrwert des in der Kunst und der Architektur berühmten Goldenen Schnitts.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.