Hemmes mathematische Rätsel: Wege zur Mitte
Der Brite W. Tom Williams war Lehrer und unterrichtete englische Literatur und schrieb auch etliche Schulbücher zu diesem Thema. Aber er hatte noch eine andere Leidenschaft: Denksportaufgaben. Unter dem Pseudonym Tantalus schrieb er in den 1930er und -40er Jahren eine wöchentliche Rätselkolumne mit dem Titel »Literary Competitions« für die englische Zeitschrift »John o' London's Weekly«. Der wohl weltweit größte Rätselerfinder Henry Ernest Dudeney verfasste von 1910 bis zu seinem Tod 1930 in der englischen Zeitschrift »The Strand Magazine« die Denksportecke »Perplexities«. Williams trat Dudeneys Erbe an und führte gemeinsam mit dem englischen Mathematiker G. H. Savage die Kolumne fort. Williams und Savage fassten ihre Rätsel auch zu vier Büchern zusammen: »The Strand Problems Book« (ca. 1940), »The Penguin Problems Book« (1940), »The Second Penguin Problems Book« (1944) und »The Third Penguin Problems Book« (1946). Das folgende Rätsel stammt aus dem »Strand Problems Book«.
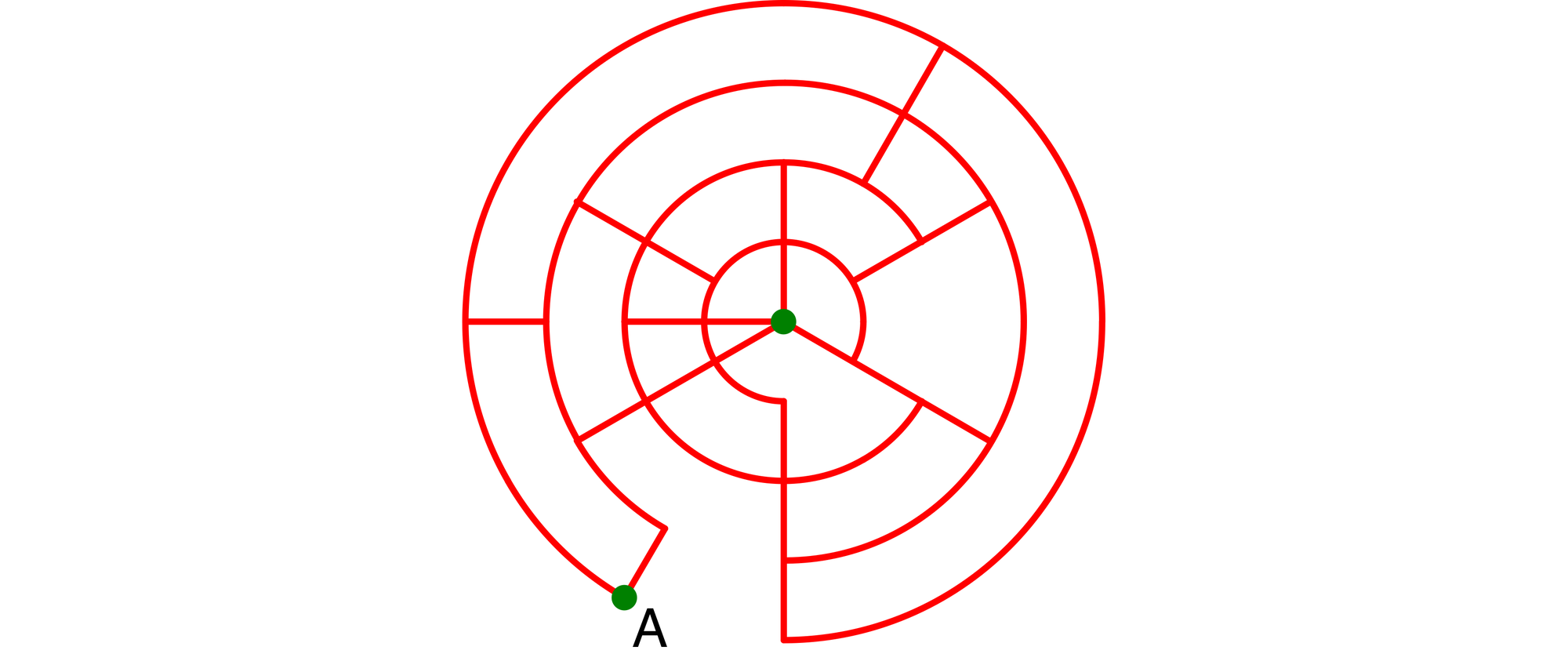
Wie viele verschiedene Wege führen vom Punkt A zum Mittelpunkt der Figur? Dabei darf man auf den gebogenen Wegen nur im Uhrzeigersinn und auf den gerade Wegen nur auf das Zentrum zugehen.
Das Rätsel ist leicht zu lösen, wenn man die möglichen Wege systematisch zählt und dabei in der Mitte beginnt. Hierzu schreibt man zunächst einmal eine 1 an den Mittelpunkt der Figur. Danach betrachtet man von innen nach außen und gegen den Uhrzeigersinn nacheinander jede Ecke, an der ein Weg abknickt oder sich verzweigt. Dabei schaut man, welche Wege man von dieser Ecke aus nehmen kann und geht sie jeweils bis zur nächsten Ecke. An den Ecken, auf die man so trifft, stehen stets bereits die Zahlen der von dort aus möglichen Wege. Diese Zahlen addiert man und schreibt sie an die betrachtete Ecke.
Man beginnt an der Ecke mit dem schwarzen Punkt. Von dort geht nur ein Weg weiter, nämlich der zum Zentrum der Figur. Dort steht eine 1. Darum wird an der schwarzen Ecke eine 1 notiert. Danach betrachtet man die Ecke mit dem grünen Punkt. Auch von dort geht nur ein Weg aus, nämlich der zur schwarzen Ecke, wo eine 1 steht. Diese 1 wird nun auch an grünen Ecke notiert. Nun folgt die Ecke mit dem blauen Punkt. Von dort gehen zwei Wege aus, der eine läuft zum Zentrum, der andere zur grünen Ecke. An beiden Ecken steht eine 1. Ihre Summe 2 wird an der blauen Ecke notiert. So hangelt man sich durch die ganze Figur und erhält schließlich, dass man vom Eingang aus 143 verschiedene Wege ins Zentrum nehmen kann.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.