Hemmes mathematische Rätsel: Wie groß ist der Radius?
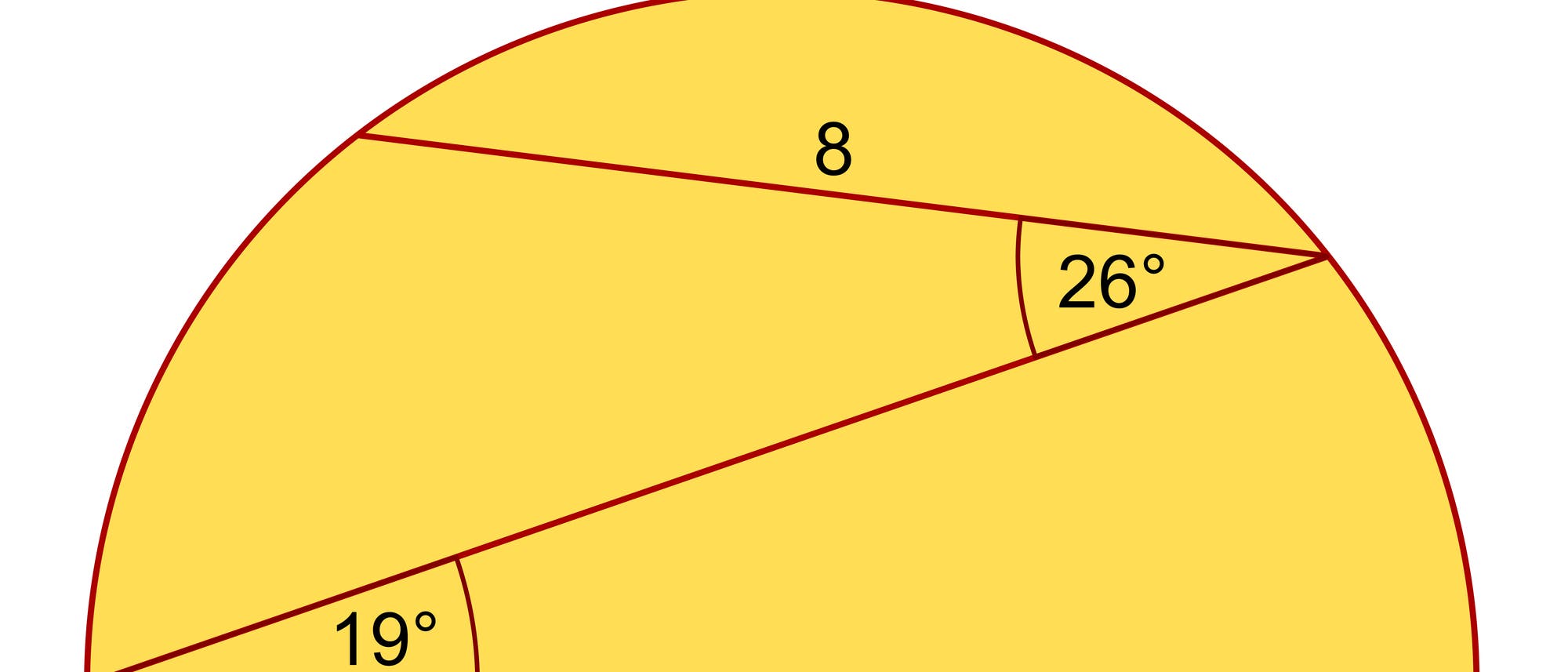
Zwei Sehnen zerschneiden einen Halbkreis in drei Teile. Zwei Winkel und die Länge einer Sehne sind bekannt. Wie groß ist der Radius des Halbkreises?
M ist der Mittelpunkt des Halbkreisdurchmessers DA. Wir ergänzen die Zeichnung durch die beiden Sehnen AB und DC sowie die beiden Radien MB und MC. Der Winkel ADB = 19 Grad ist ein Umfangswinkel über die Sehne AB. Folglich ist der Mittelpunktswinkel AMB über diese Sehne doppelt so groß und hat darum eine Größe von 38 Grad. Der Winkel BDC = 26 Grad hingegen ist ein Umfangswinkel über die Sehne DC. Somit hat der Mittelpunktswinkel MDC eine Größe von 52 Grad. Am Mittelpunkt ergänzen sich die drei Winkel CMD, BMC und AMB zu 180 Grad. Folglich hat der Winkel BMC die Größe 180 Grad – 52 Grad – 38 Grad = 90 Grad. Das Dreieck BMC ist daher rechtwinklig. Seine Katheten sind Halbkreisradien r, und seine Hypotenuse hat die Länge 8. Damit gilt nach dem Satz des Pythagoras r2 + r2 = 82 oder r = 4√2 ≈ 5,66.
Schreiben Sie uns!
Beitrag schreiben