Hemmes mathematische Rätsel: Wie lässt sich das Verhältnis errechnen?
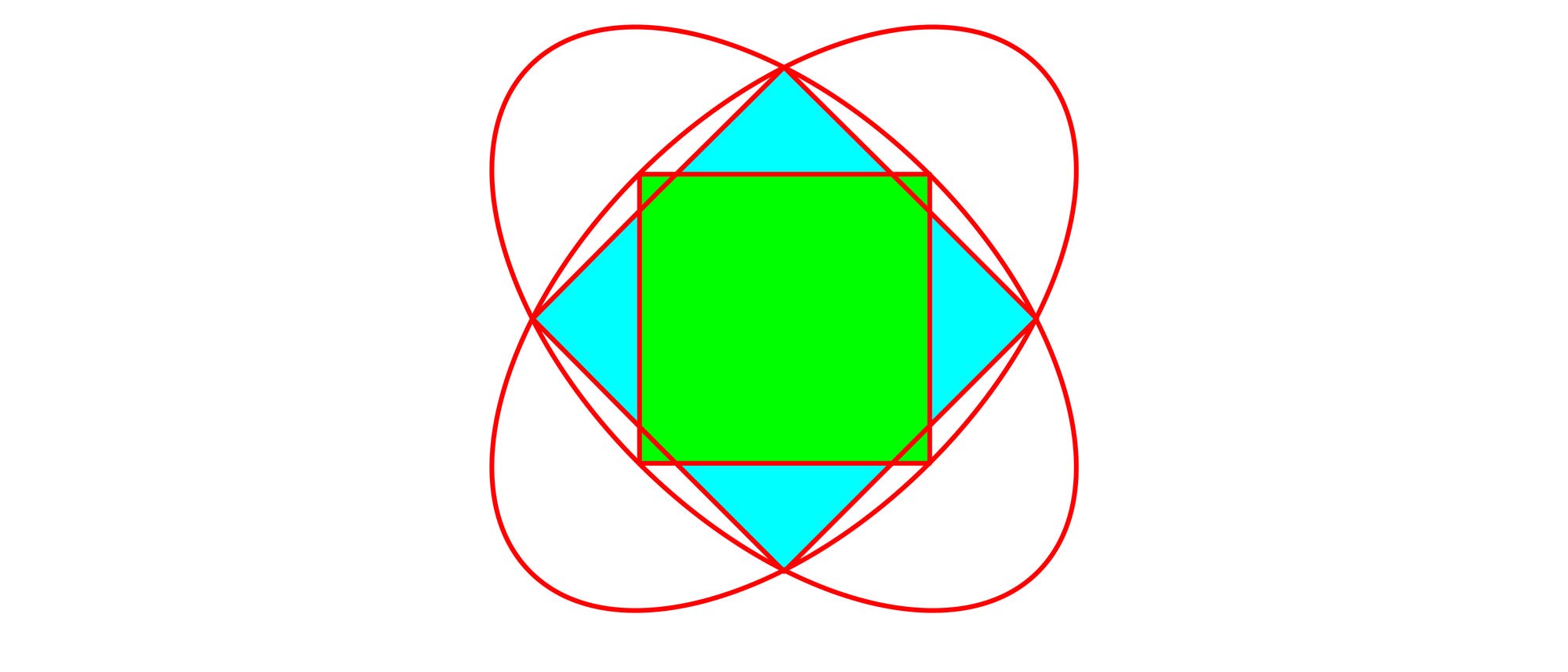
Auf den beiden Brennpunkten einer Ellipse liegen zwei sich gegenüberliegende Ecken des grünen Quadrats. Die beiden anderen Ecken des Quadrats liegen auf ihrem Umfang. Eine zweite deckungsgleiche Ellipse kreuzt die erste Ellipse so, dass ihre Achsen aufeinanderfallen. Die vier Schnittpunkte der beiden Ellipsen bilden die Ecken des blauen Quadrats. In welchem Verhältnis steht die Fläche des blauen Quadrats zu der des grünen Quadrats?
Um die Aufgabe einfach lösen zu können, drehen wir das Bild um 45° und setzen es symmetrisch in ein kartesisches Koordinatensystem. Bei Ellipsen ist der Zusammenhang zwischen der großen Halbachse a, der kleinen Halbachse b und der linearen Exzentrizität e stets a2 = b2 + e2. Wählt man die Seitenlänge des grünen Quadrats zu u = 2, ergibt sich mit dem Satz des Pythagoras b = e = √2. Daraus folgt a = 2. Für jeden Punkt der Ellipse mit den Koordinaten x und y gilt die Ellipsengleichung x2/a2 + y2/b2 = 1. Mit den konkreten Werten für a und b wird daraus x2/4 + y2/2 = 1 oder x2 + 2y2 = 4. Am Punkt P, an dem sich die Ellipsen schneiden, ist x = y. Damit wird die Ellipsengleichung zu x2 + 2x2 = 4 oder x = 2/√3. Das blaue Quadrat hat somit die Seitenlänge v = 4/√3. Das Verhältnis der Fläche des blauen Quadrats zu der des grünen Quadrats beträgt folglich v2/u2 = (16/3)/4 = 4/3.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Wie hoch ist die Wahrscheinlichkeit?
- Welche Zahl erfüllt diese Bedingungen?
- Welche Palindrome sind gesucht?
- Welches Polygon entsteht hier?
- Welche Zahl ist gesucht?
- Wie viele Ziffernfolgen gibt es?
- Welchen Flächeninhalt hat das Rechteck?
- Mit welchem Code kommt man ins nächste Level
- Wie lang ist der Durchmesser der Teller?
- Wie lautet das nächste Polynom?
- Wie kann diese Figur gebildet werden?
- Wie lang ist das rote Band?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
Beitrag schreiben