Hemmes mathematische Rätsel: Wie lässt sich diese Figur neu zusammensetzen?
© Heinrich Hemme (Ausschnitt)
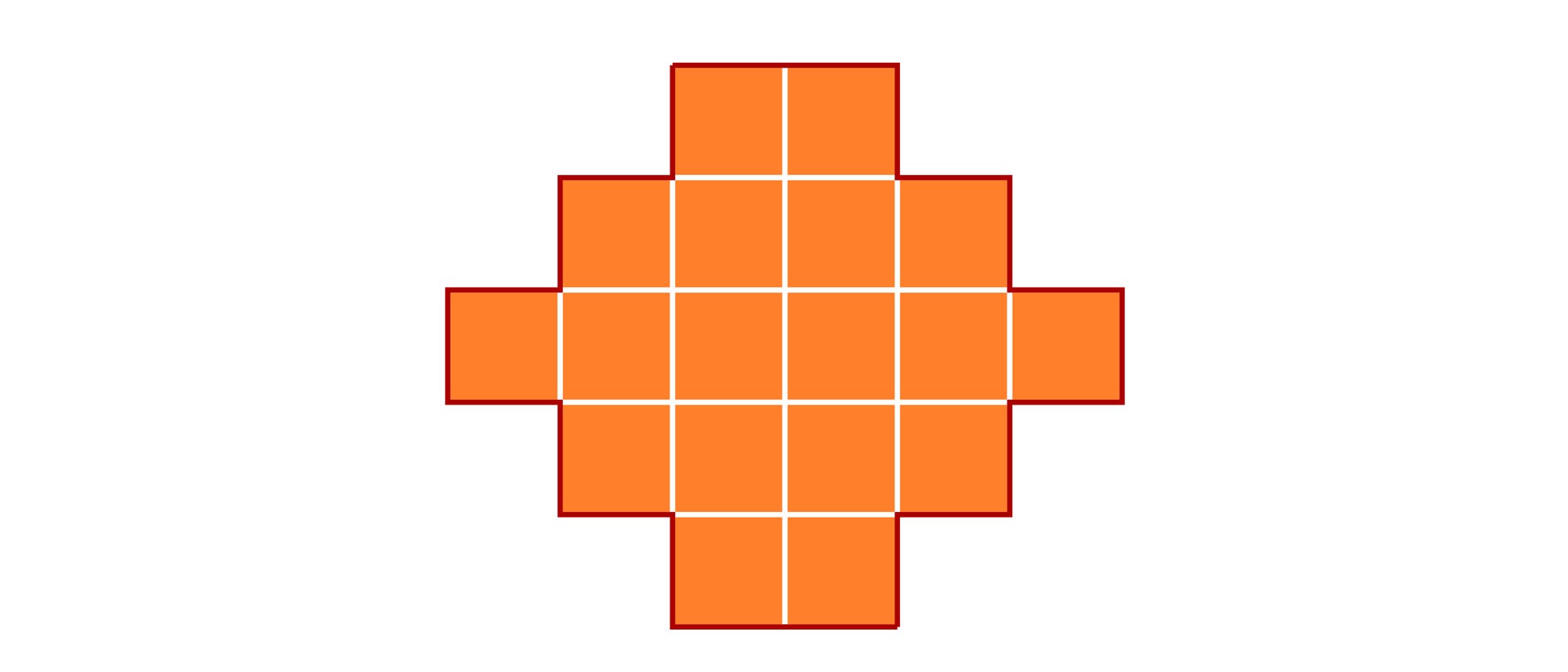
Zerlegen Sie diese Figur so in drei Teile, dass sich diese anschließend zu einem rechtwinkligen, gleichschenkligen Dreieck anordnen lassen. Die Teile dürfen dabei umgeklappt werden, um die Rückseite zur Vorderseite zu machen, sie dürfen sich aber nicht überlappen und keine Lücken in dem Dreieck lassen.
Die Ausgangsfigur besteht aus 18 Quadraten der Seitenlänge 1. Folglich muss das rechtwinklige, gleichschenklige Dreieck die Kathetenlänge 6 haben, um auf einen Flächeninhalt von 6 · 6 / 2 = 18 zu kommen. Die Hypotenuse hat die Länge von 6 Quadratdiagonalen. Somit müssen dafür drei Quadrate diagonal durchschnitten werden. Nun ist es nicht mehr schwer, eine passende Zerlegung zu finden.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben