Hemmes mathematische Rätsel: Wie lang ist die Strecke?
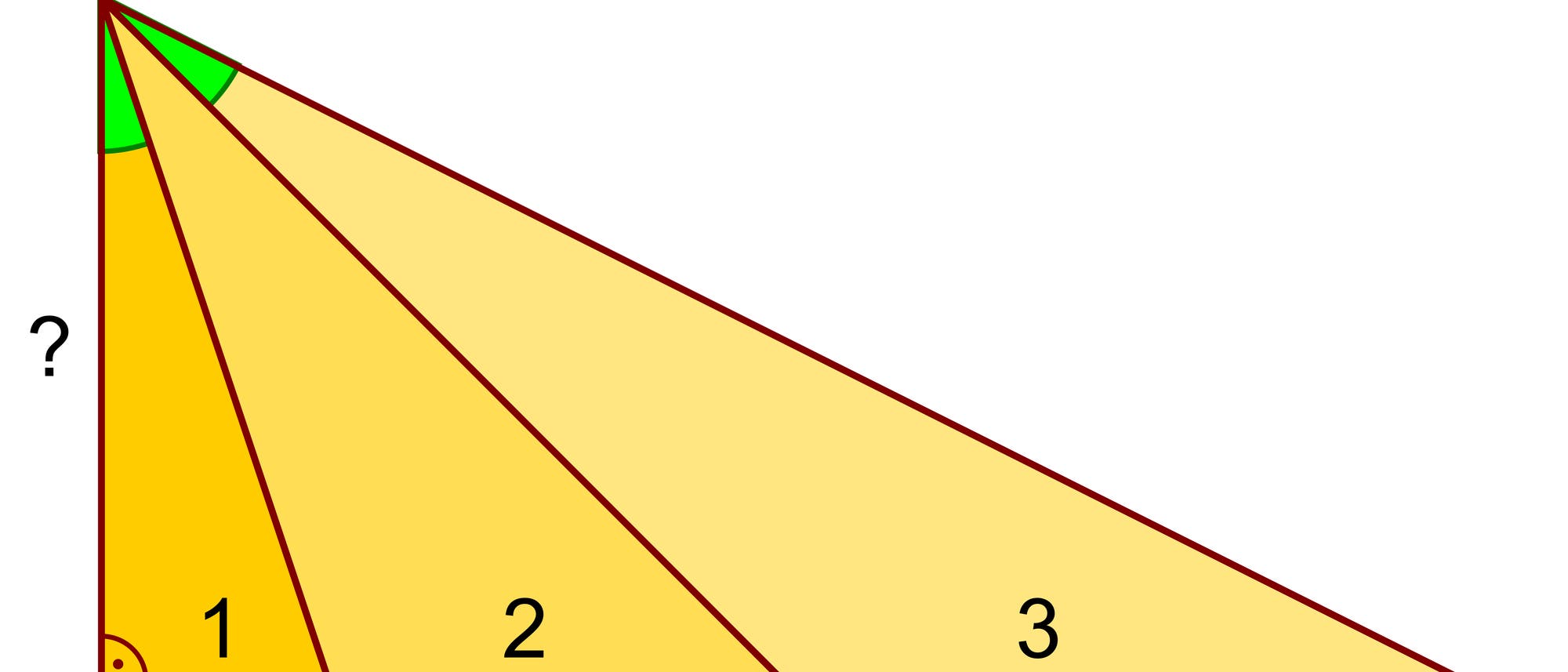
Die in der Figur grün markierten Winkel sind gleich groß. Wie lang ist die mit einem Fragezeichen versehene Strecke?
Die Zeichnung wird um zwei Kreise ergänzt. Der rote Kreis hat den Mittelpunkt N und den Radius r, und sein Umfang läuft durch die Punkte A, B und C. Der Punkt N halbiert die Strecke AC. Somit hat die Grundseitenhöhe des Dreiecks NBC die Länge x/2. Der blaue Kreis, der nur teilweise zu sehen ist, hat den Mittelpunkt M und den Radius R, und sein Umfang läuft durch die Punkte A, D und E. Der linke grüne Winkel ist ein Umfangswinkel über die Sehne BC = 1 des roten Kreises, und der rechte grüne Winkel ist ein Umfangswinkel über die Sehne DB = 3 des blauen Kreises. Da die beiden grünen Winkel gleich groß sind, gilt R/r = DE/BC = 3/1 oder R = 3r. Da die beiden Dreiecke NBC und MDF ähnlich sind, gilt ME = 3x/2. Somit gilt für das Dreieck AGM nach dem Satz des Pythagoras R2 = (9/2)2 + (x/2)2 oder (3r)2 = (9/2)2 + (x/2)2 oder 9r2 = 81/4 + x2/4. Für das Dreieck ABC gilt ebenfalls nach dem Satz des Pythagoras (2r)2 = x2 + 12 oder 4r2 = x2 + 1 oder 9r2 = 9x2/4 + 9/4. Setzt man die beiden Gleichungen für 9r2 gleich, erhält man 81/4 + x2/4 = 9x2/4 + 9/4, was man zu x = 3 vereinfachen kann.
Schreiben Sie uns!
Beitrag schreiben