Rätseln mit Eder: Wie lassen sich die Seitenlängen der Quadrate ermitteln?
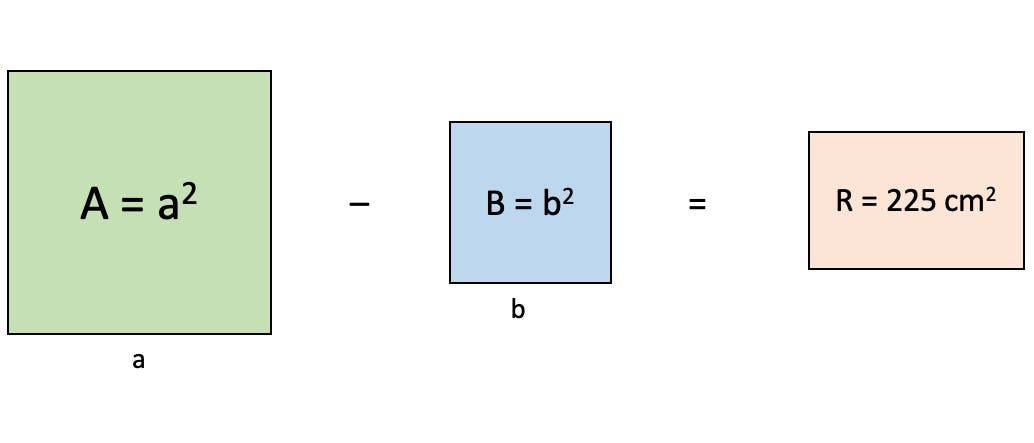
Subtrahiert man die Fläche des Quadrats B von der Fläche des Quadrats A, entsteht ein Rechteck R mit dem Flächeninhalt 225 Quadratzentimeter.
Welche Seitenlängen a und b (a > b) können die beiden Quadrate haben, wenn nur natürliche Zahlen in Frage kommen?
Es gibt vier Lösungen für die Seitenlängen a und b:
Die Differenz der beiden Quadratzahlen kann in ein Produkt umgewandelt werden:
Die Betrachtung der Teilermenge von 225 ist für die Lösung hilfreich:
Für die beiden Faktoren (a – b) und (a + b) kommen nur die folgenden Werte in Frage:
Die Werte für a und b lassen sich jetzt jeweils mit Hilfe eines Gleichungssystems finden:
Es gibt vier Lösungen für die Seitenlängen der Quadrate:
Die vier Proben bestätigen die Richtigkeit:
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Wie viele verschiedene Wege gibt es?
- Wie viele Felder werden zerstört?
- Wie viele Züge werden benötigt?
- Gibt es pythagoreische Tripel dieser Art?
- Stimmt diese Behauptung?
- Für welche Zahl steht n?
- Wie viel Prozent werden abgedeckt?
- Welche besonderen Tage werden gesucht?
- Welcher Ort ist gesucht?
- Wie groß ist die Fläche des Außenkreises?
- Wie viele Möglichkeiten gibt es, das Haus vom Nikolaus zu zeichnen?
- Wie kann das Sechseck in vier Vierecke zerlegt werden?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
Beitrag schreiben