Hemmes mathematische Rätsel: Wie viel Prozent decken die Kreise ab?
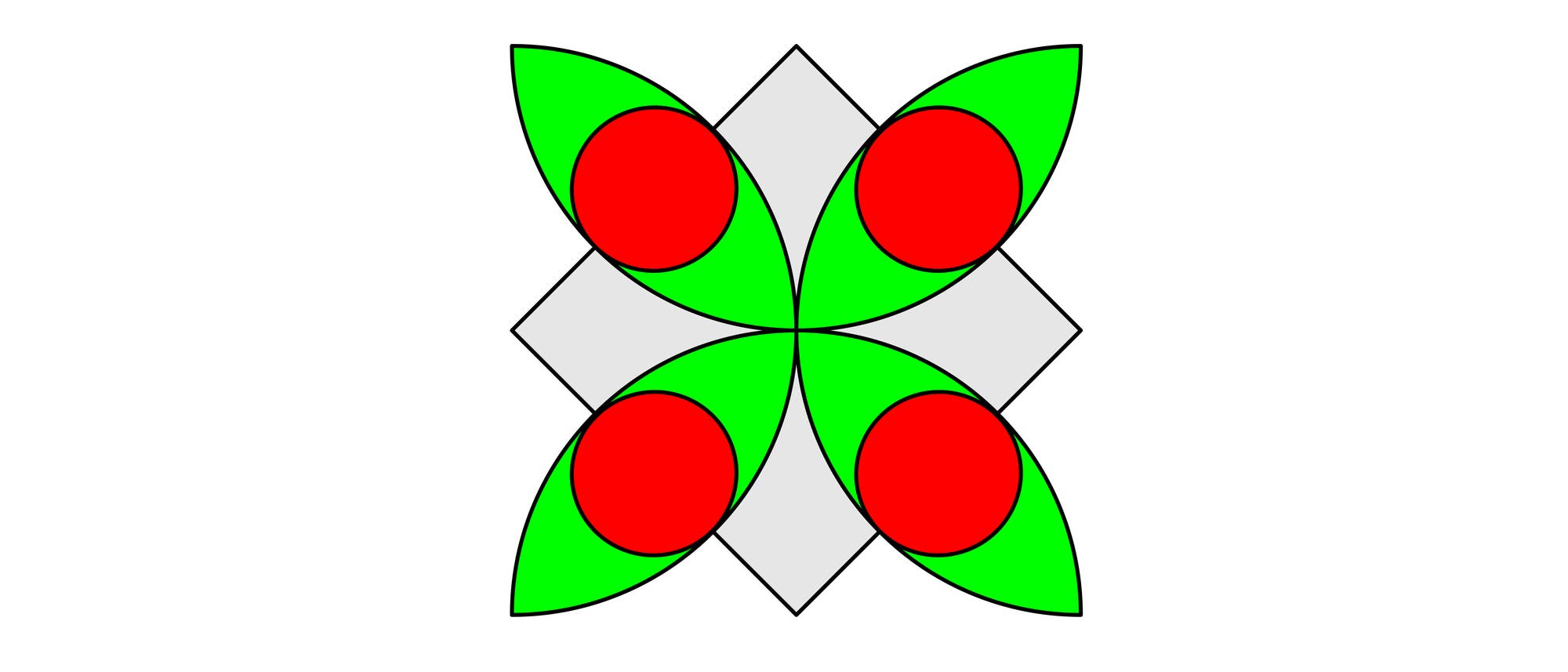
Vier gleiche Halbkreise, deren Mittelpunkte auf den Ecken eines Quadrats liegen, schneiden sich im Mittelpunkt dieses Quadrats. Die Mittelpunkte der roten Kreise fallen auf die Mittelpunkte der Quadratseiten. Wie viel Prozent der gesamten Figur werden von den roten Kreisen abgedeckt?
Der Einfachheit halber soll die Seitenlänge des Quadrats 2 betragen und das Bild um 45° gedreht werden. Die über das Quadrat hinausragenden Linsenhälften lassen sich halbieren und zusammen mit dem Quadrat zu einem Vollkreis anordnen. Der Kreisradius ist die halbe Quadratdiagonale und hat folglich die Länge R = √2. Somit hat der Kreis und damit die Figur aus der Aufgabe den Flächeninhalt πR2 = 2π.
Das zweite Bild zeigt nur einen Ausschnitt der Figur. Das Quadrat ABCD hat die Seitenlänge 1. Der Radius des roten Kreises beträgt r = ED – AD = R – 1 = √2 – 1. Folglich hat er den Flächeninhalt πr2 = π(√2 – 1)2 = π(3 – 2√2). Die vier roten Kreise decken somit einen Anteil von 4π(3 – 2√2)/2π = 2(3 – 2√2) ≈ 34,3 Prozent der Gesamtfigur ab.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Wie hoch ist die Wahrscheinlichkeit?
- Welche Zahl erfüllt diese Bedingungen?
- Welche Palindrome sind gesucht?
- Welches Polygon entsteht hier?
- Welche Zahl ist gesucht?
- Wie viele Ziffernfolgen gibt es?
- Welchen Flächeninhalt hat das Rechteck?
- Mit welchem Code kommt man ins nächste Level
- Wie lang ist der Durchmesser der Teller?
- Wie lautet das nächste Polynom?
- Wie kann diese Figur gebildet werden?
- Wie lang ist das rote Band?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
Beitrag schreiben