Hemmes mathematische Rätsel: Wie viele Züge muss der Läufer mindestens machen?
Henry Ernest Dudeney (1857–1930) war wohl der bedeutendste Rätselerfinder, der jemals lebte. Das Läuferproblem stellte er seinen Leserinnen und Lesern am 10. Mai 1896 in »The Weekly Dispatch« vor. Die Lösung erschien am 24. und am 31. Mai 1896.
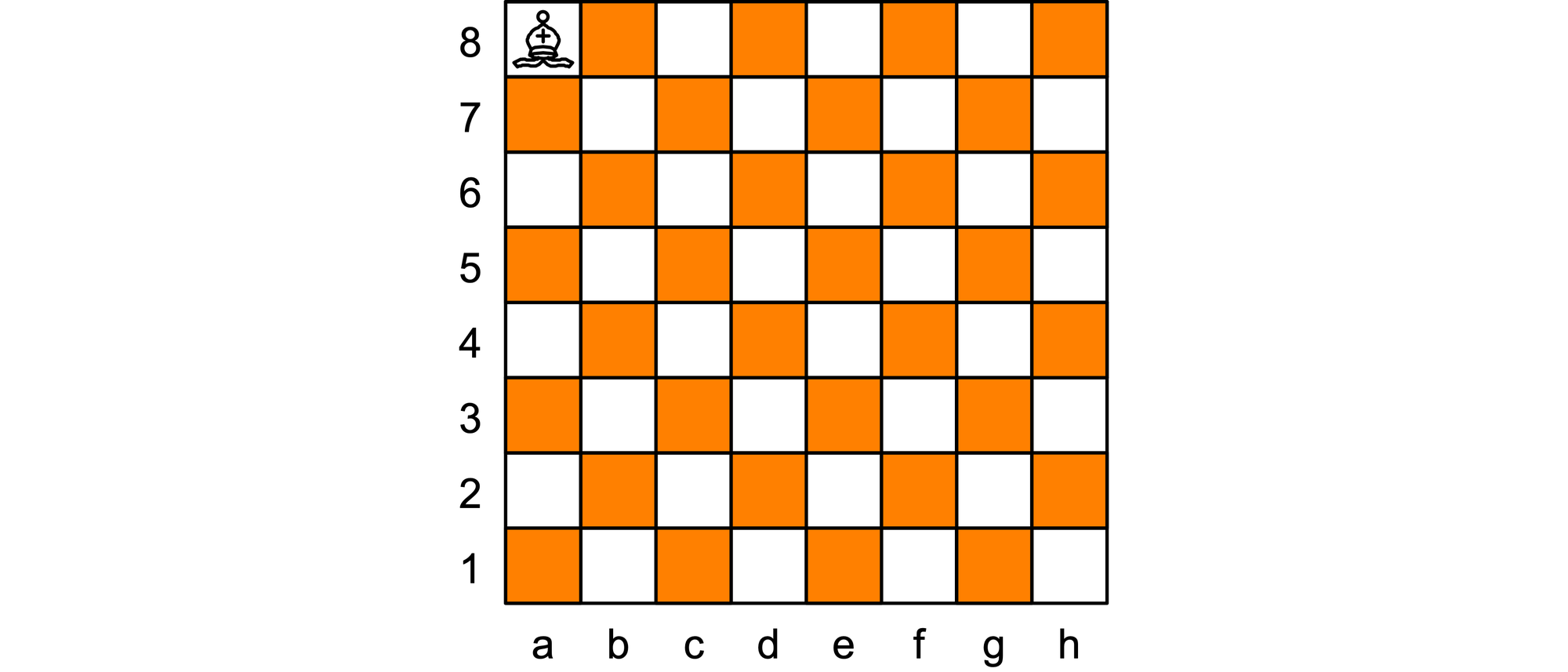
Ein Läufer steht auf dem Eckfeld a8 eines Schachbretts. Er soll mit möglichst wenigen Zügen jedes weiße Feld mindestens einmal betreten. Dabei gilt ein Feld als betreten, wenn der Läufer darüber hinweg zieht – wenn er also etwa von a8 nach c6 zieht, betritt er auch das Feld b7. Der Läufer darf bei seinem Weg über das Schachbrett jedes Feld beliebig oft betreten, aber jede Ecke, an der vier Felder zusammenstoßen, darf er höchstens einmal überqueren. Wie viele Züge muss der Läufer mindestens machen?
Der Läufer kann in 17 Zügen sämtliche weißen Felder betreten, ohne dabei jemals mehr als einmal eine Ecke zu überqueren, an der vier Felder zusammenstoßen.
Es gibt insgesamt zwei mögliche Wege, die der Läufer dazu nehmen kann, wenn man einmal von den Wegen absieht, die durch Spiegelung des Bretts an den Diagonalen oder durch Drehung um 180 Grad entstehen. Den ersten Weg hat Dudeney selbst vor über 120 Jahren gefunden, den zweiten hat der österreichische Mathematiker Helmut Postl 2005 entdeckt.
Schreiben Sie uns!
Beitrag schreiben