Wirklich homogenes Schwerefeld
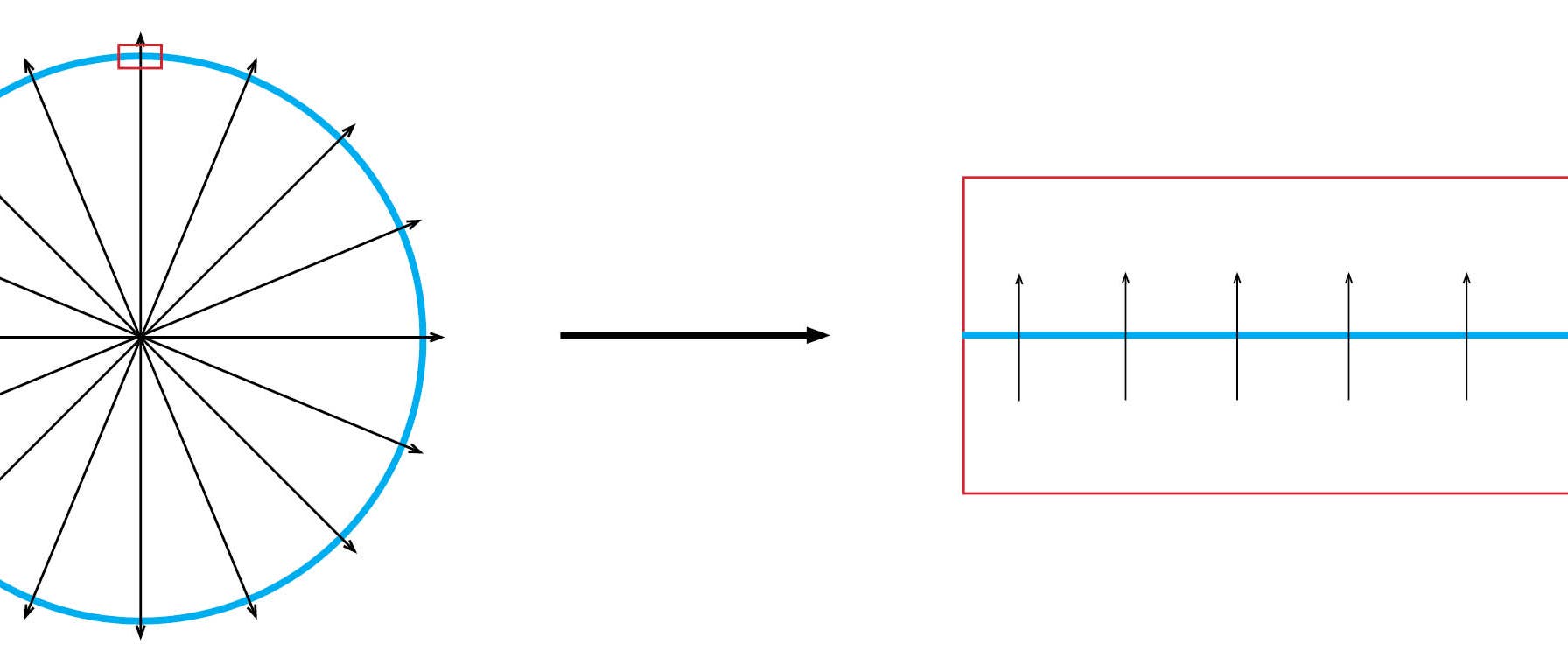
Das Schwerefeld nahe der Erdoberfläche ist ziemlich genau homogen, aber in Wirklichkeit ein Stück aus einem inhomogenen Radialfeld.
Kann es ein Objekt mit endlichen Abmessungen geben, in dem ein exakt homogenes Schwerefeld existiert (von Störungen durch die Außenwelt abgesehen)?
Es ist ein kugelförmiger Hohlraum innerhalb einer ansonsten homogenen Vollkugel.
Um das besser zu verstehen, muss man die Eigenschaften des Schwerefelds innerhalb von homogenen Voll- und Hohlkugeln kennen:
- Hohlkugel: Nach dem Satz von Gauß entspricht das Schwerefeld in ihrem Außenraum dem einer gleich schweren Punktmasse in ihrem Mittelpunkt. Andererseits kann man zeigen, dass eine konzentrische Hohlkugel in ihrem Hohlraum kein Schwerefeld erzeugt – aber auch kein von außen erzeugtes abschirmt.
- Homogene Vollkugel: Auch hier ist das Schwerefeld im Außenraum das gleiche wie das einer gleich schweren Punktmasse in ihrem Mittelpunkt. Im Innenraum hängt das Schwerefeld von ihrer Dichte ab: das Potenzial ist proportional zur Dichte und zum Quadrat des Abstandes \(\vec{r}\) des jeweiligen Ortes vom Mittelpunkt: \(V\propto \rho \vec{r}^2\).
Um das Potenzial eines kugelförmigen Hohlraums innerhalb einer Vollkugel zu berechnen, bietet es sich an, eine Überlagerung zweier Potenziale zu betrachten: das Potenzial innerhalb der großen Vollkugel plus das innerhalb einer Vollkugel an Stelle des Hohlraums mit negativer Dichte.
Wenn die Koordinaten des Mittelpunkts der großen Vollkugel \((0,0,0)\) und des Hohlraums \(\vec{a}=(a,0,0)\) sind, lauten die Potenziale der Voll- beziehungsweise Hohlkugel: \(V_{\text{Voll}}\propto \rho \vec{r}^2\) und \(V_{\text{Hohl}}\propto -\rho (\vec{r}-\vec{a})^2\). So ist das Gesamtpotenzial am Ort \(\vec{d}=(x,y,z)\) im Inneren des Hohlraums proportional zu:
\(V_{\text{ges}}(\vec{d})= V_{\text{Voll}} + V_{\text{Hohl}} \propto \rho\left[\vec{d}\vphantom{|}^2 – (\vec{d}-\vec{a})^2 \right] \) \( \propto x^2 + y^2 + z^2- (a – x)^2 – y^2 – z^2 = 2ax – a^2\)
Das Potential ändert sich also in \(y\)- und \(z\)-Richtung nicht, das heißt, es ist homogen in Richtung des Abstandes der beiden Mittelpunkte. Falls der Hohlraum konzentrisch ist, finden wir den bekannten Fall wieder, dass das Feld dort nicht nur homogen ist, sondern sogar verschwindet. Das schließt aber – wie erwähnt – nicht aus, dass ein Feld von einem anderen äußeren Objekt hier existiert: Anders als bei der Elektrizität gibt es bei der Gravitation keine Abschirmung (bei der Elektrizität geschieht sie durch Wanderung von Ladungsträgern mit passendem Vorzeichen).
Das Bild zeigt die Ortsabhängigkeit des Potenzials in einer Ebene durch beide Mittelpunkte als Zebrastreifen.
Ich muss zugeben, dass ich bis zur Lektüre in der Aufgabensammlung von Gnädig et al. (Aufgabe 110) nicht geglaubt hatte, dass es exakt homogene Schwerefelder von endlich ausgedehnten Objekten überhaupt geben kann – und schon gar nicht auf eine so einfache und schöne Art!

Schreiben Sie uns!
Beitrag schreiben