Hemmes mathematische Rätsel: Zahlen im Sechseck
Der 1949 in Berlin geborene und in München lebende Physiker Frank Gensler liebt den mathematischen Denksport und hat eine ganze Reihe hübscher Knobeleien erdacht. Auch das folgende Rätsel ist seine Erfindung und wurde 2018 in der »Aachener Zeitung«, den »Aachener Nachrichten« und der »Westdeutschen Zeitung« erstmals veröffentlicht.
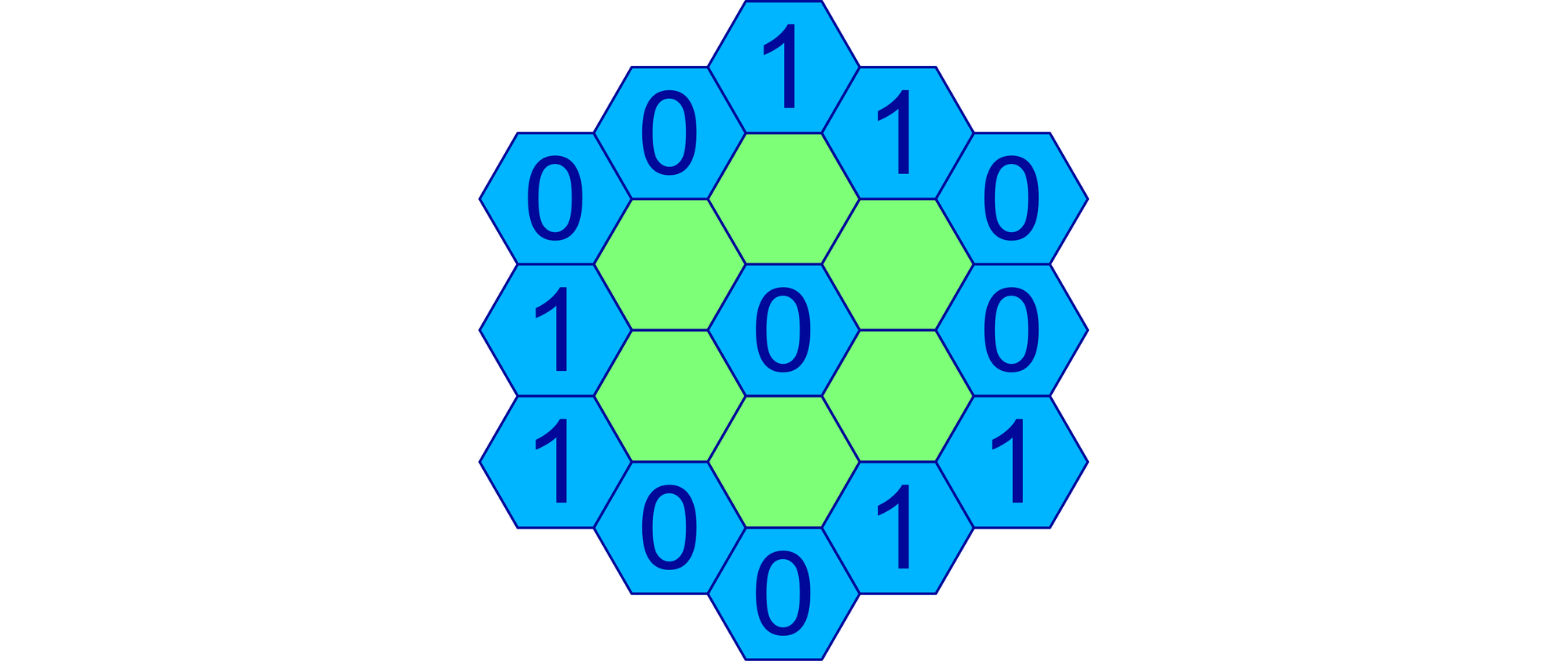
Setzen Sie sechs verschiedene positive ganze Zahlen in die grünen Felder des Wabenmusters. Die magische Konstante eines grünen Felds ist die Summe aus seiner Zahl und den Zahlen auf seinen sechs Nachbarfeldern. Die magische Konstante muss für alle grünen Felder gleich groß und so klein wie möglich sein.
In die Summe aller sechs magischen Konstanten M der sechs grünen Felder geht das gelbe Feld sechsmal ein, jedes grüne Feld dreimal, jedes rosa Feld zweimal und jedes blaue Feld einmal. Somit beträgt 6M = 6 · 0 + 3(A + B + C + D + E + F) + 2(0 + 1 + 0 + 1 + 0 + 1) + 1(0 + 1 + 0 + 1 + 0 + 1) = 3(A + B + C + D + E + F) + 9.
Die kleinstmöglichen Werte für die grünen Felder sind die Zahlen von 1 bis 6. Da sie die ganzzahlige magische Konstante M = 12 ergeben, könnten sie auch zu einer Lösung führen. Aus den magischen Konstanten der sechs grünen Felder ergeben sich die sechs Gleichungen F + A + B = 10, A + B + C = 11, B + C + D = 10, C + D + E = 11, D + E + F = 10 und E + F + A = 11. Mit je drei der Zahlen von 1 bis 6 lassen nur auf jeweils drei Weisen die Summen 10 und 11 bilden: 10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 3 + 5 und 11 = 1 + 4 + 6 = 2 + 3 + 6 = 2 + 4 + 5. Damit findet man schnell eine Lösung. Sie ist auch die einzige Lösung, wenn man einmal von symmetrischen Mustern absieht.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.