Wertmaßstab, Signaturmaßstab, E scale of a symbol, vorwiegend in thematischen Karten, aber auch in anderen graphischen Darstellungen benutztes Mittel zur Veranschaulichung von Zahlenwerten durch ihre Übertragung in die Graphische Variable Größe. Der Wertmaßstab drückt das Verhältnis zwischen dem abzubildenden Wert eines Objekts bzw. Sachverhalts in der Wirklichkeit und der Figurengröße in der Karte aus. Die wichtigsten Erscheinungsformen von Wertmaßstäben sind: Wertangabe (Punktwert) für den Einzelpunkt bei Karten nach der Punktmethode und das mathematisches Basiszahlenverhältnis (mathematische Funktion) für längen-, flächen-, volumenproportionale oder anderweitig abgebildete Mengensignaturen oder Diagrammsignaturen.
Die Festlegung von Wertmaßstäben ist immer ein Optimierungsproblem, in das insbesondere folgende Bedingungen eingehen: 1. Der Mensch vermag Längenverhältnisse recht genau, Flächenverhältnisse hingegen nur tendenziell zu beurteilen. Das Verhältnis verschiedengroßer Flächen wird i. d. R. unterschätzt . Die Schätzung von Volumenverhältnissen kann zu groben Fehlurteilen führen. Demnach wäre die lineare Abbildung gegenüber der flächenhaften zu bevorzugen und auf die pseudo-körperhafte zu verzichten. 2. Dieser allgemeinen Bedingung steht in den meisten Fällen als Bedingung das Verhältnis V des größten zum kleinsten darzustellenden Wert





entgegen. V wird in der Statistik auch als Wertespanne beschrieben und kann die Größenordnung von 10⁴ bis 10⁵ erreichen (z. B. 2 · 10⁴ bei N_max =2 Mio. und N_min =100 Einwohnern (Ew.)). 3. Die für die Darstellung nutzbare Kartenfläche ist i. d. R. zu klein, um ein großes Werteverhältnis längen- oder flächenproportional wiedergeben zu können, denn es ist eine bestimmte, noch wahrnehmbare Mindestgröße l_min oder F_min vorauszusetzen. 4. Die Lagebeziehungen der Objekte im Georaum werden durch die Verortung der Signaturen, Figuren bzw. Diagramme an ihrem Bezugspunkt modelliert. In Dichtegebieten führt dies zur Überlagerung der Kartenzeichen. 5. Unübersichtliche Signaturballungen lassen sich durch Verdrängung, Freistellung und gezielte Überlagerung von großen mit kleinen Kartenzeichen lesbar gestalten. Die Möglichkeiten einer solchen "visuellen Entflechtung" sind jedoch beschränkt, sodass u. U. die einzige Alternative in der Anpassung des Wertmaßstabs besteht. 6. Die Kartenbelastung geht als weiteres allgemeines Kriterium in die Optimierung des Wertmaßstabs ein. 7. Nicht zuletzt sind semantisch-assoziative Aspekte dahingehend zu berücksichtigen, dass beispielsweise längenproportionale Darstellungen möglichst nur für Daten bzw. Sachverhalte genutzt werden, die in der Wirklichkeit des Georaums eindimensional sind, flächenproportionale Darstellungen für Sachverhalte, die in der Realität auch Flächen sind oder flächenhaft angeordnet auftreten usw.
Die Wahl des Wertmaßstabs, genauer die Annäherung an sein Optimum, erfolgt unter Berücksichtigung sämtlicher genannten Aspekte, auch durch ihre Wertung im Hinblick auf den Zweck der Karte. Sie gestaltet sich vergleichsweise unkompliziert bei Werteverhältnissen von V > 10², die längenproportional darstellbar sind. Für das lineare Maß l einer geometrischen Figur mit dem zugehörigen Merkmalswert N gilt:
l = k · N (2), wobei





l₀ ist der Einheitswert, d. h. die Länge der Grundeinheit, z. B. 1 mm, N_o die Maßstabsbasis, der Mengenwert, der dem Einheitswert zugeordnet ist.
Für V < 10² wurden verschiedene Ansätze und Formeln entwickelt. Strenge Flächenproportionalität lässt sich jedoch bei V < 10³ nicht mehr erreichen.
Da jedoch der Flächenvergleich ohnehin unsicher ist (vgl. 1. Bedingung), wird die Unterscheidbarkeit der Größen der Kartenzeichen häufig durch Festlegung von Größenklassen (Größenstufen) hergestellt, denen jeweils eine bestimmte Klasse von Merkmalswerten zugeordnet ist. Auch gestufte Wertmaßstäbe lassen sich für V > 10² annähernd flächenproportional gestalten, z. B. als Proportionalität der Größenstufen zum jeweiligen Mittelwert der Klassen. Jedoch ist darauf zu achten, dass die Kartenzeichen benachbarter Größenstufen (Flächen) auch im Kartenzusammenhang eindeutig unterscheidbar sind.
Für die graphische Veranschaulichung von Zahlenwerten in der Karte stehen somit flächenproportionale und nichtflächenproportionale, kontinuierliche und gestufte Wertmaßstäbe zur Verfügung. Die Berechnung von kontinuierlichen Wertmaßstäben beginnt mit der Ermittlung von V nach (1). Lässt der Wert von V darauf schließen, dass eine flächenproportionale Darstellung möglich ist, stehen zwei Verfahren zur Wahl:
a) aufgrund von Erfahrung oder Überschaubarkeit des Problems wird einer gebräuchlichen Flächeneinheit F₀ ein runder Einheitswert N₀ des darzustellenden Merkmals zugeordnet, z. B. könnte 1 mm² Signaturfläche 100 Ew. repräsentieren. Daraus ergibt sich die Maßstabskonstante k





Zugleich gelten





und





Durch Auflösen von (4) nach F_min und (5) nach F_max zur Berechnung der kleinsten bzw. der größten Signaturfläche lässt sich prüfen, ob k für die betreffende Karte verwendbar oder zu modifizieren ist.
b) Der zweite Ansatz besteht darin, durch Schätzen oder überschlägiges Berechnen die kleinste oder die größte Signaturfläche festzulegen und nach (4) bzw. (5) eine vorläufige Maßstabskonstante k' zu ermitteln. Mit k' lässt sich die jeweils andere Extremfläche bestimmen. Fällt F_min zu klein bzw. F_max zu groß aus oder soll eine möglichst einprägsame Maßstabskonstante gefunden werden, wird die Berechnung mit entsprechend korrigierten Werten für die Extremflächen wiederholt und ihre Darstellbarkeit geprüft.
Ist der nach a) oder b) ermittelte Wertmaßstab verwendbar, berechnen sich die Flächen sämtlicher Signaturen nach
F =k · N (6)
Ergibt ein flächenproportionaler Wertmaßstab nach a) oder b) wegen eines V nahe 10^2,5, wegen absehbarer starker Überlagerung von Signaturen oder zu hoher allgemeiner Kartenbelastung kein befriedigendes Ergebnis, muss zu einem nichtflächenproportionalen Wertmaßstab übergegangen werden.
Für nichtflächenproportionale Wertmaßstäbe stehen mehrere Formeln zur Verfügung, deren Anwendung mit unterschiedlichen Vor- und Nachteilen behaftet ist, die dem Zweck der Karte entsprechende Kompromisse erfordern. Generell gilt, dass man sich mit zunehmendem V (< 10³) von der Flächenproportionalität entfernt. Dieser Nachteil kann meist zugunsten der Erfüllung anderer Bedingungen, vor allem von 6., akzeptiert werden.
Sämtliche Formeln für nichtflächenproportionale Wertmaßstäbe setzen die Festlegung von F_min und F_max voraus. Verbreitet wird die Formel von G.  Jensch angewendet:
F = k · N^b (7.1)
Dabei ist





und





Wertmaßstäbe sind wichtiger Bestandteil der Legende. Kontinuierliche Wertmaßstäbe können als Kurve veranschaulicht werden, an der sich sämtliche Signaturgrößen der Karte abgreifen oder abmessen lassen. Für gestufte Wertmaßstäbe ist die Ausweisung sämtlicher in der Karte auftretenden Signaturgrößen mit Angabe der Klassengrenzen (vgl. Klassenbildung) zwingend erforderlich.
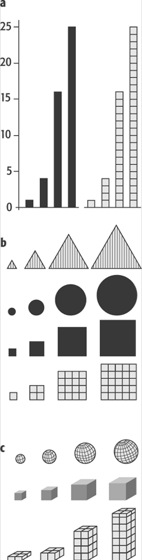
Neben der Angabe der Basiszahl (Maßstabsbasis) für Mengen ist bei flächen- und volumenproportionaler Darstellung die zusätzliche Veranschaulichung der benutzten graphischen Figuren in ausgewählten Größenstufen eine wesentliche Erleichterung für die richtige Auffassung (Schätzung) der Proportionen der Figuren des Karteninhalts (Abb.).
In Kartenkonstruktionsprogrammen und Geoinformationssystemen sind Funktionen zur Auswahl und Berechnung des Wertmaßstabs implementiert. Steht ein genügend breites Spektrum der oben erläuterten oder vergleichbarer Berechnungsgrundlagen zur Verfügung, wird damit der Auswahl- und Bewertungsprozess bis zur endgültigen Version der Darstellung wesentlich erleichtert und beschleunigt (Tab.).

KGR

Literatur: [1] GROSSER, K. (1987): Theoretische Grundlagen und Algorithmen zur rechnergestützten Gestaltung von Signaturmaßstäben einschließlich entsprechender Legenden. Leipzig, 15-40. [2] TÖPFER, F. (1974): Kartographische Generalisierung. Gotha/Leipzig.

Wertmaßstab (Tab.):Wertmaßstab (Tab.): Vor- und Nachteile der Hauptarten von Wertmaßstäben.

Wertmaßstab:Wertmaßstab: Größenverhältnisse verschiedener Figuren. Die vier Figuren jeder Gruppe verhalten sich wie 1:4:16:25; a) lineare Figur (eindimensional), b) flächenhafte Figuren (zweidimensional), c) räumliche Figuren (dreidimensional).