Login erforderlich
Dieser Artikel ist Abonnenten mit Zugriffsrechten für diese Ausgabe frei zugänglich.
Serie Mathematik (Teil IV): Elliptische Kurven und eine kühne Vermutung
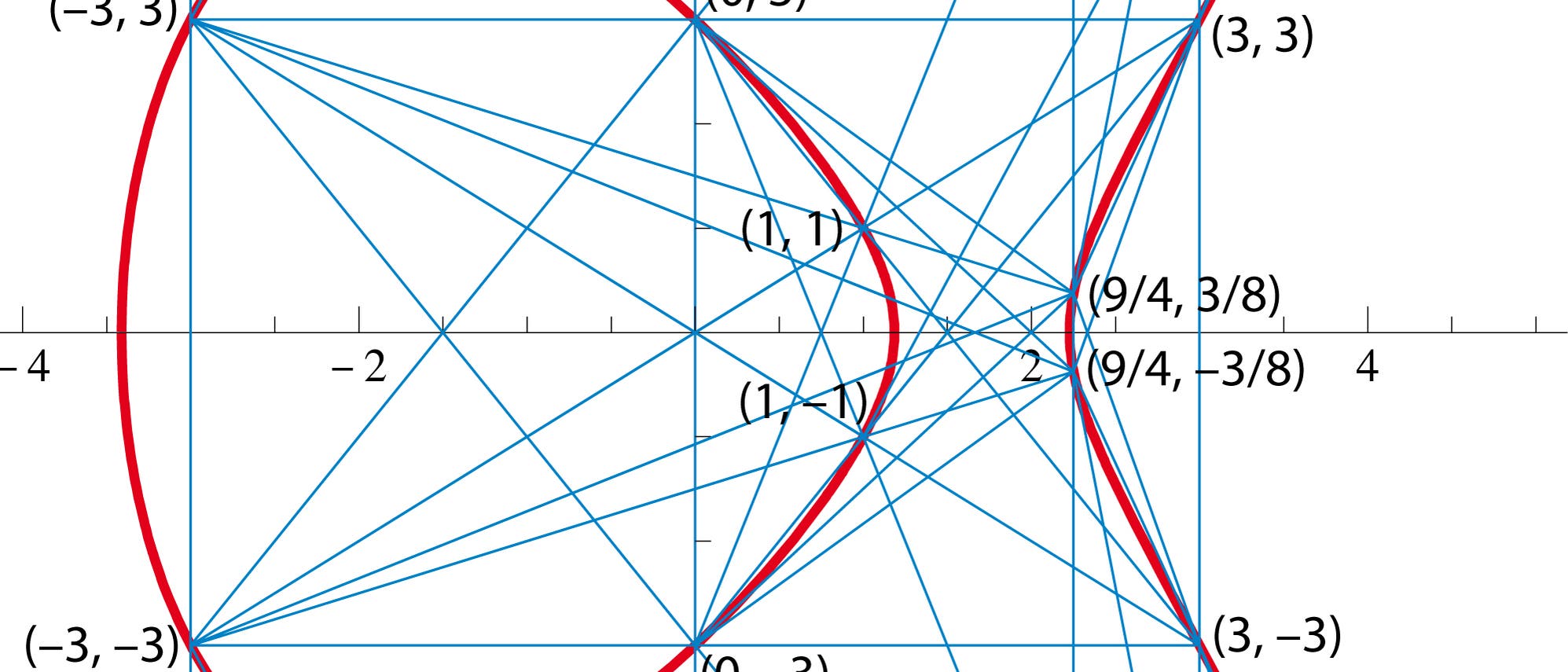
© Christoph Pöppe (Ausschnitt)
Die erste Begegnung mit den so genannten elliptischen Kurven ist
für den Außenstehenden wenig
erhellend. Sie werden von den
Mathematikern ins Leben gerufen durch eine
verwirrend erscheinende Definition; dennoch
entpuppen sie sich unter den geduldigen Bemühungen der Fachleute als zentrale Knoten
in einem weit gespannten Gedankennetz und
helfen so, überraschende Verbindungen zu
anderen Bereichen herzustellen.
Ein spektakuläres Beispiel ist der Beweis der legendären fermatschen Vermutung durch Andrew Wiles und Richard Taylor, bei dem elliptische Kurven die entscheidende Rolle spielen (Spektrum der Wissenschaft 8/1993, S. 14, und 1/1998, S. 96). Darüber hinaus finden sie Verwendung für viele zahlentheoretische Probleme, darunter das hartnäckige Kongruenzzahlproblem: Für welche natürlichen Zahlen n gibt es ein rechtwinkliges Dreieck mit rationalen Seitenlängen und Flächeninhalten?
Mehr noch: Elliptische Kurven besitzen auch praktische Anwendungen (was für einen Zahlentheoretiker allerdings nicht das vorrangige Kriterium ist, um den Wert seiner Tätigkeit zu beurteilen). Dank einer merkwürdigen algebraischen Struktur, die man auf ihnen findet, kann man Funktionen konstruieren, die leicht berechenbar, aber ohne eine Zusatzinformation praktisch nicht umkehrbar sind...
Ein spektakuläres Beispiel ist der Beweis der legendären fermatschen Vermutung durch Andrew Wiles und Richard Taylor, bei dem elliptische Kurven die entscheidende Rolle spielen (Spektrum der Wissenschaft 8/1993, S. 14, und 1/1998, S. 96). Darüber hinaus finden sie Verwendung für viele zahlentheoretische Probleme, darunter das hartnäckige Kongruenzzahlproblem: Für welche natürlichen Zahlen n gibt es ein rechtwinkliges Dreieck mit rationalen Seitenlängen und Flächeninhalten?
Mehr noch: Elliptische Kurven besitzen auch praktische Anwendungen (was für einen Zahlentheoretiker allerdings nicht das vorrangige Kriterium ist, um den Wert seiner Tätigkeit zu beurteilen). Dank einer merkwürdigen algebraischen Struktur, die man auf ihnen findet, kann man Funktionen konstruieren, die leicht berechenbar, aber ohne eine Zusatzinformation praktisch nicht umkehrbar sind...
Schreiben Sie uns!
Beitrag schreiben