Magische Quadrate gibt es im Überfluss. Die Aufgabe lautet: Man fülle die Zahlen von 1 bis n² in ein quadratisches Schema von n · n Feldern ein, so dass die Summe über jede Zeile, jede Spalte und über beide Diagonalen stets dieselbe ist. Es gibt zahlreiche Anleitungen zu ihrer systematischen Lösung und noch viel mehr Lösungen, die einfach durch Probieren zu Stande kommen – je größer die Quadratseite n, desto mehr.

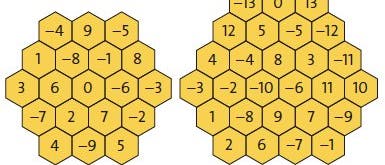
Nun ist das Quadrat nicht die einzige Form, mit der man die Ebene lückenlos bepflastern kann. Da regelmäßige Sechsecke, im bekannten Bienenwabenmuster angeordnet, ein hübsches Bild abgeben, haben viele Leute nach einem »magischen Sechseck« gesucht, also einer Anordnung aus – zum Beispiel – 19 Sechsecken in Reihen der Längen 3, 4, 5, 4, 3, die derart mit den Zahlen von 1 bis 19 belegt werden, dass alle »Reihensummen« gleich sind (Bild unten, a). Dabei verläuft eine »Reihe« entweder waagerecht, schräg ansteigend oder schräg abfallend. Aus einer solchen Anordnung von Bienenwaben (einem »Sechseckssechseck«) kann man eine größere machen, indem man sie allseits mit einem Ring von Sechsecken umgibt. Das Verfahren ist beliebig wiederholbar; die so konstruierten Sechseckssechsecke haben sämtlich ungerade Seitenlängen...