Kuhn-Tucker-Bedingung, bezeichnet eine wichtige Eigenschaft von gewissen Punkten \(\bar{x}\) aus dem Zulässigkeitsbereich eines Optimierungsproblems, die bei der Suche nach Extremalpunkten eine zentrale Rolle spielt.

Es sei das Minimum einer Funktion f ∈ C¹(ℝⁿ, ℝ) (also einer reellwertigen Funktion aus C¹(ℝⁿ)) unter der Nebenbedingung x ∈ M gesucht. Dabei hat M die übliche Form \begin{eqnarray}M:=\{x\in {{\mathbb{R}}}^{n}|{h}_{i}(x)=0,i\in I;{g}_{j}(x)\ge 0,j\in J\}\end{eqnarray} mit endlichen Indexmengen I und J und Funktionen h_i, g_j ∈ C¹(ℝⁿ, ℝ). Ein Punkt \(\bar{x}\in M\) erfüllt die Karush-Kuhn-Tucker-Bedingung, sofern es reelle Zahlen \({\bar{\lambda }}_{i},i\in I,\text{und}\,{\bar{\mu }}_{j},j\in {J}_{0}(\bar{x})\) gibt (wobei \begin{eqnarray}{J}_{0}(\bar{x}):=\{j\in J|{g}_{j}(\bar{x})=0\}),\end{eqnarray} die die folgenden Bedingungen erfüllen: \begin{eqnarray}Df(\bar{x})=\displaystyle \sum _{i\in I}{\bar{\lambda }}_{i}\cdot D{h}_{i}(\bar{x})+\displaystyle \sum _{j\in {J}_{0}(\bar{x})}{\bar{\mu }}_{j}\cdot D{g}_{j}(\bar{x})\end{eqnarray} und \begin{eqnarray}{\bar{\mu }}_{j}\ge 0\,\mathrm f\ddot{\mathrm u}\mathrm r\, \text {alle}\,j\in {J}_{0}(\bar{x}).\end{eqnarray}

Unter Gültigkeit gewisser Regularitätsbedingun-gen, wie zum Beispiel der linearen Unabhängig-keitsbedingung, erfüllen lokale Minimalpunkte vonf|_M immer die Karush-Kuhn-Tucker-Bedingung.

Letztere läst sich auch in der Form \begin{eqnarray}Df(\bar{x})=\displaystyle \sum _{i\in I}{\bar{\lambda }}_{i}\cdot D{h}_{i}(\bar{x})+\displaystyle \sum _{j\in J}{\bar{\mu }}_{j}\cdot D{g}_{j}(\bar{x}),\end{eqnarray}\begin{eqnarray}{\bar{\mu }}_{j}\cdot (\bar{x})=0,\end{eqnarray}\(\bar{\mu }\geqq 0\) für alle j∈ J schreiben. Da man hier für alle Indizes j ∈ J↗Lagrange-Multiplikatoren\({\bar{\mu }}_{j}\) betrachtet, mußzusätzlich die Komplementaritätsbedingung \({\bar{\mu }}_{j}\cdot \)\({g}_{j}(\bar{x})=0\)j ∈ J erfüllt sein.

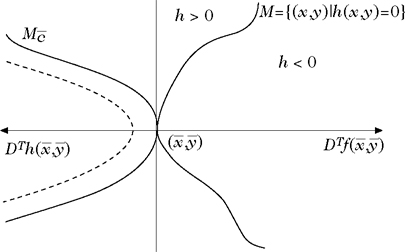
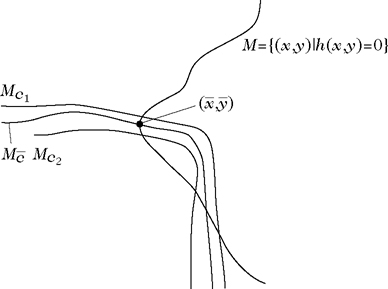
Als geometrische Veranschaulichung der Karush-Kuhn-Tucker-Bedingung betrachte man eine differenzierbare Abbildung f :ℝ² → ℝ und eine Nebenbedingung h(x, y) = 0 mit differenzierbarem h :ℝ² → ℝ. Es sei \((\bar{x},\bar{y})\) ein lokaler Extremalpunktvon f|_M, wobei \begin{eqnarray}M:=\{(x,y)\in {{\mathbb{R}}}^{2}|h(x,y)=0\}\end{eqnarray} ist. Die Gültigkeit der linearen Unabhängigkeitsbedingung in \((\bar{x},\bar{y})\) bedeutet grad h\((\bar{x},\bar{y})\) ≠ 0 ∈ ℝ²; somit ist die Menge M lokal durch einen Parameter parametrisierbar (Satz über implizite Funktionen). Betrachtet man die Niveaulinien \begin{eqnarray}{M}_{c}:=\{(x,y)\in {{\mathbb{R}}}^{2}|f(x,y)=0\}\end{eqnarray} von f für c ∈ ℝ,so besagt die Karush-Kuhn-Tucker-Bedingung anschaulich, daß die Niveaulinie \({M}_{\bar{c}}\)für \(\bar{c}:=f(\bar{x},\bar{y})\) die Kurve M berühren muß (Abbildung a)). Andernfalls würden alle die Niveaulinien M_c für Werte c, die nahe genug bei \(\bar{c}\) liegen, die Kurve M transversal schneiden (Abbildung b)). Da dies sowohl für Werte c > \(\bar{c},\) als auch für solche < \(\bar{c}\) gelte, könnte dann \((\bar{x},\bar{y})\) kein lokaler Extremalpunkt von f|M sein.