Lexikon der Mathematik: Rayleigh-Verteilung
bei gegebenem Parameter σ > 0 das durch die Wahrscheinlichkeitsdichte
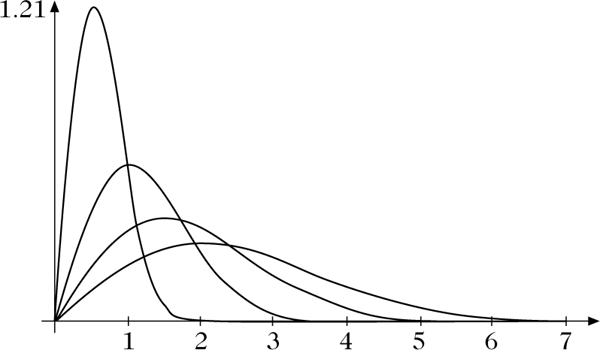
Dichten der Rayleigh-Verteilungen mit Parametern σ = 0.5(0.5)2.0
Besitzt die Zufallsvariable X eine Rayleigh-Verteilung mit dem Parameter σ > 0, so gilt für den Erwartungswert \(E(X)=\sigma \sqrt{\pi /2}\) und für die Varianz \(Var(X)=\frac{1}{2}{\sigma }^{2}(4-\pi )\). Der Modalwert liegt an der Stelle x = σ, und der Median ist \(m=\sigma \sqrt{\mathrm{ln}\,4}\). Die Rayleigh-Verteilung ist eine spezielle Weibull-Verteilung.
Anwendungen der Rayleigh-Verteilung finden sich z. B. in den Ingenieurwissenschaften, wo sie etwa zur Modellierung der Lebensdauer von schnell alternden Bauteilen verwendet wird.
Schreiben Sie uns!