Lexikon der Mathematik: Traktrix
Schleppkurve, Hundekurve, die Kurve, die ein Gegenstand, etwa ein an einer Schnur befestigter Stein im Sand, beschreibt, wenn man diesen an der Schnur hinter sich herzieht, und dabei geradlinig in eine Richtung geht, die von der Richtung der Verbindungslinie zum Stein abweicht.
Auf diesem Modell beruht der deutsche Name Schleppkurve. Auch die Namen „Hundekurve“ oder „Verfolgungskurve“ sind prägnante Bezeichnungen, denn eine sehr anschauliche Vorstellung von der Traktrix ist durch den Weg eines Hundes gegeben, der aus seitlicher Richtung kommend ein in geradliniger Richtung fliehendes Beutetier verfolgt und zu diesem dabei konstanten Abstand behält (was für den Hund eher frustrierend ist).
Eine Parameterdarstellung der Traktrix erhält man wie folgt: Man lege einen Stab der Länge a so auf die (x, y)-Ebene, daß sich sein Anfangspunkt A im Koordinatenursprung O = (0, 0) und sein Endpunkt B auf der x-Achse im Punkt (a, 0) befinden. Bewegt man dann A entlang der y-Achse, so beschreibt B eine Kurve, deren zwischen dem jeweiligen Kurvenpunkt und der y-Achse gelegenen Tangentenabschnitte von dem Stab gebildet werden und daher sämtlich die gleiche Länge a haben.
Daraus kann man den Anstieg der Tangente errechnen. Man erhält die Gleichung
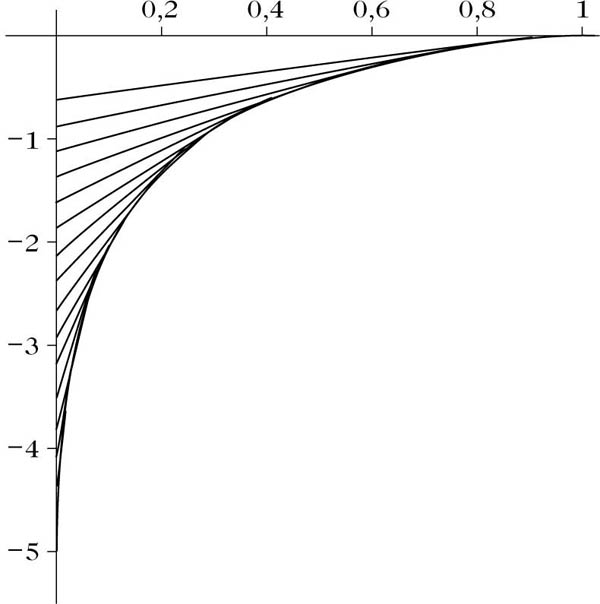
Traktrix mit Tangentenabschnitten konstanter Länge 1.
Die Fläche, die die Traktrix bei Rotation um die y-Achse überstreicht, ist die Pseudosphäre, das älteste und einfachste Beispiel einer Fläche konstanter negativer Gaußscher Krümmung. Die Evolute der Traktrix ist eine Kettenlinie.
Schreiben Sie uns!