Lexikon der Mathematik: Vektorraumbündel
Vektorbündel, ein gefaserter topologischer Raum π : V → B, derart, daß jede Faser Vb = π−1(b); b ∈ B; ein endhchdimensionaler reeller oder komplexer Vektorraum N, und die Faserung lokal-trivial ist.
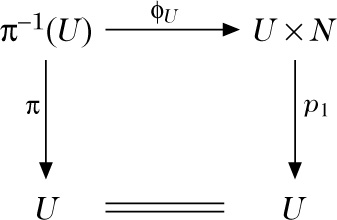
Dies bedeutet: V und B sind topologische Räume und π ist eine stetige surjektive Abbildung. V heißt TotaIraum und B Basis des Vektorraumbündels. Jeder Punkt b ∈ B der Basis besitzt eine offene Umgebung U ⊆ B, und es gibt einen Vektorraum N, derart, daß π−1(U) ⊆ V linear isomorph als Faserbündel zu U × N ist. Der lokale lineare Isomorphismus kann gegeben werden durch ϕU : π−1 (U) → U × N, so daß p1 ○ ϕU = π gilt (p1U × W → U sei die Projektion auf die erste Komponente des Produkts)
Linearität bedeutet die Forderung, daß
Meist wird die Basis als zusammenhängend angenommen. In diesem Fall folgt automatisch, daß die Dimension des Vektorraums Vb unabhängig vom Basispunkt b ist. Diese Dimension heißt Rang oder Dimension des Vektorraumbündels. Vektorraumbündel vom Rang 1 heißen Geradenbündel (manchmal auch Linienbündel genannt).
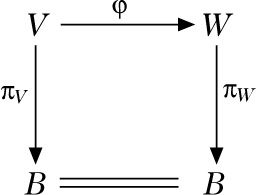
Seien πV : V → B und πW : W → B Vektorraumbündel über derselben Basis B. Eine stetige Abbildung ϕ : V → W heißt Vektorraumbündelmorphismus (oder einfach Vektorbündelmorphismus), falls
- das folgende Diagramm kommutiert:
d. h., es gilt πWφ = πV, bzw. die Faser Vb, wird nach der Faser Wb, abgebildet, und© Springer-Verlag GmbH Deutschland 2017Bild vergrößern - die Faserabbildung φ|Vb : Vb → Wb, linear ist.
Sei π : V → B ein Vektorraumbündel. Eine Teilmenge V′ ⊆ V heißt Unterbündel, falls π′ = π|V′ : V′ → B ein Vektorraumbündel ist, und jede Faser π−1(b) ∩ V′ ein Untervektorraum von Vb, ist. Ist ein solches Unterbündel gegeben, dann trägt der topologische Raum, den man durch faserweise Quotientenbildung erhält, eine kanonische Vektorraumbündelstruktur V/V′ → B. Dieses Bündel heißt Quotientenbündel.
Alle universellen Konstruktionen für Vektorräume, wie etwa Summe, Tensorprodukt, symmetrisches Produkt, Dualraum, äußeres Produkt, Homomorphismen zwischen zwei Vektorräumen, etc., haben ihre Entsprechung bei den Vektorraumbündeln durch „faserweise Definition“. Die Konstruktion erfolgt mit den lokalen Trivialisierungen. Dies sei für den Fall der Summe V ⊗ W näher erläutert. Sei U eine genügend klein gewählte offene Menge, über der die Bündel V und W gemeinsam trivialisieren. Ist etwa das Bündel V lokal isomorph zu U × N und W lokal isomorph zu U × M, dann ist die Vektorraumbündelsumme V ⊕ W das Bündel, das lokal isomorph zu U × (N⊕M) ist. Diese Summe heißt manchmal auch Whitney-Summe.
Sind f : B′ → B eine stetige Abbildung und π : V → B eine Vektorraumbündel über B, so ist dadurch kanonisch das Pullbackbündel f*V → B′ gegeben. Es wird lokal wie folgt erhalten. Ist V lokal isomorph über U ⊆ B zum trivialen Bündel U × N, so ist f*V lokal isomorph zum Bündel f−1(U) × N über f−1(U) ⊆ B. Anschaulich: über dem Punkt b′ ∈ B′ wird der Vektorraum \({V}_{f(b^{\prime})}\) „angeheftet“.
Ein Vektorraumbündel V vom Rang n kann durch einen stetigen 2-Kozykel mit Werten in der Gruppe GL(n, ℝ) bzw. GL(n, ℂ) gegeben werden. Sei \({\{{U}_{i}\}}_{i\in J}\) eine offene Überdeckung von B, derart daß V über jedem Ui trivial wird, und seien
Die Abbildung
- ψii = In,
- ψijψji = In auf Ui ∩ Uj ≠ ø,
- ψijψjk = ψik auf Ui ∩ Uj ∩ Uk ≠ ø. (In ist die n-dimensionale Einheitsmatrix).
Zwei 2-Kozykel (ψij) und \(({\psi}^{\prime}_{ij})\) heißen kohomolog, falls es stetige Funktionen
Umgekehrt wird durch die Vorgabe einer Überdeckung {Ui}i∈j von B und eines zugeordneten 2-Kozykels (ψij) von stetigen Funktionen durch Zusammenkleben der Ui × ℝn (bzw. Ui × ℂn) entlang der Ui ∩ Uj mit Identifikation der Fasern über x ∈ Ui ∩ Uj mit Hilfe der Matrizen ψij(x) ein Vektorraumbündel definiert.
Ist ein Vektorraumbündel π : V → B vom Rang n gegeben, dann ist für jede offene Teilmenge U ⊆ B die Menge der Schnitte \({\mathcal{V}}(U)\) über U definiert als
Der Raum \({\mathcal{V}}(B)\) heißt Raum (oder Modul) der globalen Schnitte des Vektorraumbündels V. Das System der \(U\to {\mathcal{V}}(U)\) definiert eine Garbe von Vektorräumen bzw. eine Garbe von Moduln über der Garbe der stetigen Funktionen auf B. Als Garbe von Moduln ist sie lokalfrei vom Rang n (die Basis B sei als zusammenhängend vorausgesetzt).
Garben sind allgemeinere Objekte, die allerdings innerhalb der Theorie der Vektorraumbündel ebenfalls benötigt werden. Ist etwa φ : V → W ein Vektorraumbündelmorphismus, so ist die Teilmenge
Alles, was hier für topologische Vektorraumbündel durchgeführt wurde, kann in völlig analoger Weise für differenzierbare Vektorraumbündel über differenzierbaren Mannigfaltigkeiten, für holomorphe Vektorraumbündel über komplexen Mannigfaltigkeiten, und für algebraische Vektorraumbündel über algebraischen Varietäten gemacht werden. Die beteiligten Abbildungen sind in der jeweiligen Kategorie zu wählen. Ein wichtiges differenzierbares Vektorraumbündel wird für jede differenzierbare Mannigfaltigkeit durch das Tangentialbündel gegeben.
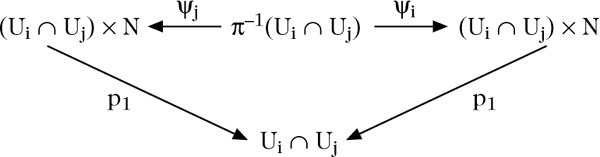
Schreiben Sie uns!