Lexikon der Mathematik: konvexe Menge
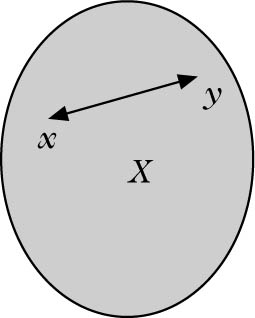
Teilmenge X eines reellen Vektorraums V, die mit je zweien ihrer Punkte auch deren Verbindungsstrecke enthält, d. h. es gilt
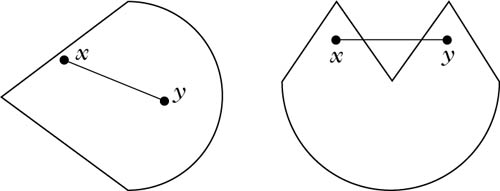
Eine konvexe (links) und eine nicht konvexe Menge (rechts).
Für alle x, y ∈ V ist z. B. [x, y] konvex, und alle Unterräume von V sind konvex. Die konvexen Teilmengen von ℝ sind genau die Intervalle. Bilder und Urbilder konvexer Mengen unter linearen Abbildungen sind konvex. Für α ∈ ℝ und konvexe X, Y ⊂ V sind das skalare Vielfache
und die Summe
konvex. Ist X konvex, so enthält X auch jede Konvexkombination von Elementen aus X. Eine Menge X ⊂ V ist genau dann konvex, wenn
<?PageNum _197
gilt. Die Vereinigungsmenge einer Kette (d. h. einer durch Inklusion linear geordneten Menge) konvexer Mengen ist konvex. Das kartesische Produkt und der Durchschnitt beliebig vieler konvexer Mengen sind konvex. Auf letzerem gründet sich die Definition der konvexen Hülle einer Menge als Durchschnitt all ihrer konvexen Obermengen.
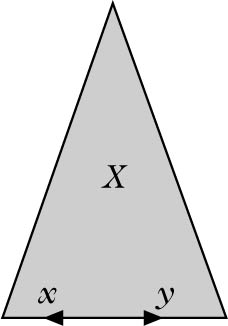
Man nennt eine Teilmenge X eines topologischen Vektorraums V streng konvex, wenn die offene Verbindungsstrecke je zweier Punkte aus X im Inneren von X liegt, also genau dann, wenn
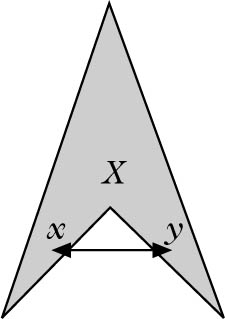
gilt, wobei (x, y) = [x, y] \{x, y} sei. Jede streng konvexe Menge ist offenbar konvex, aber nicht umgekehrt. Jede konvexe Menge ist offensichtlich sternförmig, jedoch nicht umgekehrt.
streng konvex
konvex, nicht streng konvex
sternförmig, nicht konvex
Die Untersuchung der Eigenschaften konvexer Mengen ist ein Gegenstand der konvexen Analysis. Von besonderer Bedeutung sind konvexe Kegel und konvexe Polyeder.
Schreiben Sie uns!