Die Menschheit muss sich fürchten: Eine außerirdische Zivilisation, die der »Trisolarier«, nähert sich der Erde, weil ihr eigener Heimatplanet dem Untergang geweiht ist – und die Trisolarier kommen nicht in Frieden. Sie stammen aus einem fernen Sonnensystem mit drei Sonnen, deren Flugbahnen keiner exakten Regel zu folgen scheinen. Die Gesellschaften auf dem dazugehörigen Planeten werden immer wieder ausgelöscht, wenn eine der Sonnen zu nah an ihn heranreicht oder alle drei Sterne so weit entfernt sind, dass eine zerstörerische Eiszeit einsetzt. Diese Geschichte schildert der chinesische Sciencefiction-Autor Liu Cixin in seinem Bestseller-Roman »Die drei Sonnen«, der aktuell auch als Serie verfilmt wird.

Selbst wenn es sich hierbei (zum Glück!) um eine fiktive Geschichte handelt, hat die zu Grunde liegende Physik durchaus Hand und Fuß: Unser benachbartes Sternsystem Alpha Centauri besteht beispielsweise aus drei Sternen und enthält mindestens einen Planeten (HD 131399). Der Teil mit der außerirdischen Bevölkerung scheint allerdings nicht zuzutreffen – zumindest haben wir bisher keinen Hinweis darauf, dass es auf HD 131399 Leben gibt.

Und tatsächlich besitzt das so genannte Dreikörperproblem keine allgemeine Lösung. Das heißt, man kann das Verhalten eines Sternsystems mit drei Sonnen meist nicht exakt vorhersagen. Ein sie umkreisender Planet bildet dabei ein viertes Objekt, so dass man für das Gesamtsystem ein »Vierkörperproblem« lösen müsste, um dessen verworrene Umlaufbahnen zu bestimmen.

Ein mehr als 300 Jahre altes Problem

Dass diese Aufgabe solche Schwierigkeiten bereitet, erscheint auf den ersten Blick erstaunlich. Denn schon im Jahr 1687 veröffentlichte der Gelehrte Sir Isaac Newton sein berühmtes Werk »Philosophiæ Naturalis Principia Mathematica«, das die Bewegungsgleichungen von Objekten und das inzwischen nach ihm benannte Gravitationsgesetz enthält. Erstere besagen, dass ein Objekt durch eine darauf einwirkende Kraft beschleunigt wird, während das Gravitationsgesetz erklärt, wie sich zwei Massen durch die Schwerkraft gegenseitig anziehen. Indem man beide Formeln miteinander verbindet, kann man herausfinden, wie ein Objekt durch die Gravitationskraft beschleunigt wird.

Zudem hatte Newton damals (etwa zeitgleich mit Leibniz) die Differenzialrechnung begründet. Demnach lässt sich eine Ableitung, wie man sie aus der Schule kennt, als Änderung einer Größe interpretieren. Die zeitliche Ableitung einer Bahnkurve x(t) entspricht der Geschwindigkeit v(t) eines Objekts. Das lässt sich verstehen, indem man die zeitliche Änderung der Bahnkurve ^Δx⁄_Δt = v betrachtet und die zeitliche Änderung Δt immer kleiner werden lässt. Für den Grenzfall, dass Δt gegen null geht, erhält man schließlich ^Δx⁄_Δt = ^dx⁄_dt = v. Wenn man wiederum die zeitliche Änderung der Geschwindigkeit betrachtet, erhält man die Beschleunigung eines Objekts – die Beschleunigung entspricht also der zweiten Ableitung der Bahnkurve.

So ermöglichen es die newtonschen Gleichungen, aus einer Kraft, die auf ein Objekt wirkt, dessen Bahnkurve zu ermitteln. Damit begründete der Gelehrte das Gebiet der Mechanik: Plötzlich ließ sich die Bewegung von allerlei Objekten vorhersagen, etwa wenn man einen Ball wirft oder einen Apfel von einem Baum fällt. Damit ließ sich auch die Umlaufbahn der Erde um die Sonne bestimmen – wodurch Newton die keplerschen Gesetze bestätigen konnte.

Erde und Sonne: Das Zweikörperproblem

Betrachtet man zunächst bloß die Sonne und unseren Planeten, lassen sich die newtonschen Gleichungen nutzen, um deren Bahnkurven zu berechnen. Einerseits wissen wir, dass die Erde infolge der auf sie wirkenden Gravitationskraft F_G beschleunigt wird: F_G = m_Erde·a_Erde, wobei m_Erde der Masse der Erde und a_Erde ihrer Beschleunigung entspricht. Andererseits lässt sich die Gravitationskraft F_G zwischen Sonne und Erde ebenfalls mit Hilfe der newtonschen Formeln berechnen: F_G = G·(m_Erde·m_Sonne)/r². Hier bezeichnet G die Gravitationskonstante, m_Sonne die Masse der Sonne und r den Abstand zwischen Sonne und Erde.

Möchte man die Umlaufbahn der Erde um die Sonne berechnen, muss man also bloß beide Gleichungen gleichsetzen: m_Erde·a_Erde = G·(m_Erde·m_Sonne)/r². Nun kann man die Tatsache ausnutzen, dass die Beschleunigung a_Erde der zweiten zeitlichen Ableitung der Bahnkurve der Erde x entspricht. Andererseits ist der Abstand r zwischen Sonne und Erde durch die Differenz der Aufenthaltsorte von Erde (x) und Sonne (y) gegeben: m_Erde·(d²x/dt²) = G·(m_Erde·m_Sonne)/(x−y)². Da auf beiden Seiten der Gleichung der Faktor m_Erde auftaucht, kann man diesen streichen, um die Gleichung zu vereinfachen: d²x/dt² = G·m_Sonne/(x−y)². Folglich hat man eine Gleichung, die von zwei Unbekannten abhängt, nämlich von x und y. Falls Sie sich an den Mathematik-Unterricht zurückerinnern, dann wissen Sie: Das lässt sich so nicht lösen. Sie brauchen eine weitere Gleichung, um die Bahnkurven zu bestimmen.

Glücklicherweise gibt es noch eine zweite Gleichung. Denn wir haben bisher völlig außer Acht gelassen, dass die Erde ebenso eine – wenn auch sehr geringe – Anziehungskraft auf die Sonne ausübt, nämlich F_G = m_Sonne·a_Sonne. Auch hier kann man die newtonsche Gleichung für die Gravitationskraft einsetzen und erhält: m_Sonne·(d²y/dt²) = G·(m_Erde·m_Sonne)/(x−y)². Die Gleichung lässt sich wieder vereinfachen, indem man auf beiden Seiten m_Sonne kürzt: d²y/dt² = G·m_Erde/(x−y)².

Aus physikalischer Sicht ergibt es Sinn, dass man ein System aus zwei Gleichungen lösen muss. Durch die Schwerkraft der Sonne folgt die Erde einer Umlaufbahn – andersherum bewegt sich die Sonne ein wenig durch den Einfluss der Gravitationskraft der Erde. Wenn sich aber beide Objekte bewegen, verändert sich ihr Abstand und damit auch die Stärke der Gravitationskraft, die mit dem Quadrat der Entfernung abnimmt. Deshalb muss man beide Bewegungen berücksichtigen, um die Umlaufbahn des Systems zu berechnen.

Damit haben wir alles, was wir brauchen: zwei Gleichungen mit zwei Unbekannten x und y. Die Schwierigkeit besteht nun darin, dass es sich nicht um gewöhnliche Gleichungen handelt, die man einfach nach x oder y auflösen kann, sondern um Differenzialgleichungen: Es tauchen auch Ableitungen der beiden Variablen x und y auf. Solche Gleichungssysteme haben nicht immer eine exakt darstellbare Formel als Lösung.

Im Fall zweier Körper haben wir allerdings Glück: Mit ein paar mathematischen Tricks lässt sich eine exakte Lösung angeben. Die entsprechenden Bahnkurven haben in diesem Fall stets die Form eines Kegelschnitts. Das heißt, sie folgen entweder der Form einer Parabel, einer Hyperbel, eines Kreises oder einer Ellipse – abhängig von den Parametern des Problems (Anfangsgeschwindigkeit, Masse und so weiter). Die ersten beiden Fälle beschreiben ein ungebundenes System: etwa, wenn ein Asteroid in die Nähe der Sonne kommt, von ihrer Masse abgelenkt wird und dann wieder in der Tiefe des Alls verschwindet. Ellipsen- und kreisförmige Bahnen entsprechen hingegen einem gebundenen System, wie es für die acht Planeten unseres Sonnensystems der Fall ist.

In seinem imposanten Werk hatte Newton genau diese Fälle durchgespielt und exakt beschrieben. Der nächste logische Schritt bestand darin, sich Systemen mit drei Objekten zuzuwenden, etwa Sonne-Erde-Mond. Doch das führte schnell zu Schwierigkeiten.

Das System Sonne-Erde-Mond lässt sich nicht lösen

Der Ansatz ist zunächst der gleiche wie zuvor: Man stellt für alle drei Körper die newtonschen Bewegungsgleichungen auf. Nun »spüren« die Objekte aber jeweils zwei Gravitationskräfte: Die Erde spürt die Anziehung von Mond und Sonne, der Mond wird von Sonne und Erde angezogen und die Sonne nimmt die Schwerkraft von Erde und Mond wahr. Damit ergibt sich ein System aus drei Gleichungen:

m_Mond·a_Mond = F^Erde_G + F^Sonne_G
m_Erde·a_Erde = F^Mond_G + F^Sonne_G
m_Sonne·a_Sonne = F^Mond_G + F^Erde_G

Schreibt man die Gleichungen aus, erhält man drei Differenzialgleichungen, die von den Variablen x (Bahnkurve Erde), y (Bahnkurve Sonne) und z (Bahnkurve Mond) abhängen. In diesem Fall hat man jedoch weniger Glück als im Fall mit bloß zwei Objekten: Das Dreikörperproblem stellt sich als unlösbar heraus. Sprich: Es gibt keine allgemein gültige Formel für x, y und z, welche die drei Differenzialgleichungen stets erfüllt. Und genau das ist auch das Problem der fiktiven Trisolarier, die in Liu Cixins Roman aus diesem Grund ihr Sonnensystem verlassen müssen.

Bedeutet das nun, dass man keinerlei Umlaufbahnen berechnen kann, sobald mehr als zwei Objekte betroffen sind? Das wäre höchst erschreckend: Denn einerseits besteht ja unser Sonnensystem aus mehr als zwei Objekten. Andererseits folgen auch Teilchen, die einander elektrisch anziehen, einem ähnlichen Gesetz wie der Schwerkraft (hier nimmt die Kraft ebenfalls mit dem Quadrat der Entfernung ab). Wenn sich das Verhalten all dieser Systeme nicht vorhersagen ließe, bliebe uns ein Großteil der Details über die uns umgebende Welt verborgen.

Näherungslösungen und Spezialfälle

Zum Glück stellt sich die Realität als nicht ganz so dramatisch dar. Kurz nach der Veröffentlichung von Newtons Arbeit konnten Mathematiker und Physiker zeigen, dass unser Sonnensystem höchstwahrscheinlich stabil ist: Es wird sich also nicht plötzlich vollkommen verrückt verhalten und einen Planeten ausstoßen. Diese Befürchtung hatte kurzzeitig bestanden. Pierre-Simon Laplace konnte aber zusammen mit Joseph Louis Lagrange im 18. Jahrhundert das Mehrkörperproblem unseres Sonnensystems zumindest näherungsweise lösen, indem die beiden den großen Massenunterschied zwischen der Sonne und den übrigen Planeten ausnutzten. Wie die beiden Gelehrten erkannten, ist die Anziehungskraft der Sonne so stark, dass sie die Planeten dauerhaft an sie bindet.

Auf diese Weise lässt sich auch das Dreikörperproblem von je zwei leichten Planeten und der Sonne näherungsweise lösen. Wenn zwei Massen verschwindend klein sind, kann man ihren Einfluss auf die Sonne vernachlässigen und bloß eine leichte Störung der Umlaufbahn untereinander berücksichtigen. Eine solche Untersuchung des Uranus führte Mitte des 19. Jahrhunderts zur Vorhersage des bis dahin noch unbekannten Planeten Neptun. Astronomen hatten erkannt, dass Uranus einer ungewöhnlichen Bahnkurve folgte, weshalb sie annahmen, ein anderer Planet in seiner Nähe müsse ihn beeinflussen. Indem sie das Dreikörperproblem (Sonne, Uranus und dritter Planet) näherungsweise berechneten, konnten sie vorhersagen, wo im Sternenhimmel ein weiterer Planet lauern könnte. Mit dieser Information gelang es schließlich, den achten Planeten, der heute als Neptun bekannt ist, zu finden.

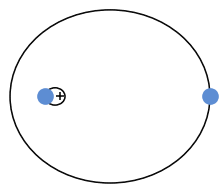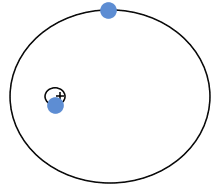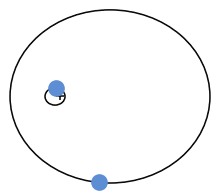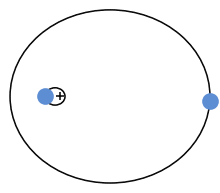
Es gibt aber auch Spezialfälle, für die sich das Dreikörperproblem exakt lösen lässt. 1767 fand der Schweizer Mathematiker Leonhard Euler erstmals solche Lösungen: Dabei handelt es sich um drei Körper, die zu jedem Zeitpunkt eine gerade Linie bilden. Wenn zwei der drei Körper die gleiche Masse haben, muss man die dritte Masse bloß in der Mitte zwischen ihnen platzieren. Schon hat man ein System geschaffen, das diese lineare Anordnung stets beibehalten wird. Euler konnte zudem zeigen, dass es für jede Massenverteilung geeignete Anordnungen gibt, wodurch ein solches gebundenes lineares System existiert.

Sechs Jahre später fand Lagrange weitere gebundene Umlaufbahnen, die das Dreikörperproblem exakt lösen. In diesem Fall bilden die drei Massen zu jedem Zeitpunkt ein gleichseitiges Dreieck. Auch er konnte nachweisen, dass eine solche Lösung nicht nur für drei gleiche Massen existiert, sondern für jede Art von Körper. Die Spezialfälle von Lagrange und Euler sind bis heute die einzigen bekannten exakten Lösungen des Dreikörperproblems, die als in sich geschlossene Formel darstellbar sind.

Haltet die Druckerpressen an!

Der nächste große Fortschritt auf dem Gebiet ereignete sich erst 100 Jahre später, als der Mathematiker Gösta Mittag-Leffler 1885 zu Ehren des 60. Geburtstags des schwedischen und norwegischen Königs Oskar II. einen Wettbewerb ausrief: Er präsentierte vier Aufgaben, deren Lösung mit 2500 schwedischen Kronen belohnt wurden. Eine der Fragen drehte sich um das N-Körper-Problem: Man sollte für ein System aus N Massenpunkten jeweils eine unendlich lange Summe angeben, durch die sich die Bahnkurve eines Objekts näherungsweise berechnen lässt.

Mittag-Leffler war bekannt, dass es keine allgemeine Lösungsformel zum Mehrkörperproblem gab. Aber er wusste auch, dass sich manche Phänomene durch unendlich lange Summen zumindest näherungsweise bestimmen lassen. Falls die Summanden schnell genug schrumpfen, nimmt die gesamte Summe einen endlichen Wert an – im Fall der ausgeschriebenen Aufgabe würde die Summe zu jedem Zeitpunkt eine endliche Zahl liefern, die dem Aufenthaltsort des beschriebenen Objekts entspricht.

Niemandem gelang es, eine solche Reihe zu finden. Doch unter den Einreichungen, die in den folgenden drei Jahren eingingen, stach die Arbeit von Henri Poincaré heraus. Der französische Mathematiker hatte darin neue Methoden eingeführt, um das Problem zu untersuchen. Um über die theoretischen Ansätze hinaus auch ein konkretes Ergebnis beizusteuern, widmete er sich einem Spezialfall des Dreikörperproblems, bei dem eine der Massen so klein ist, dass ihr Einfluss auf die anderen beiden quasi vernachlässigt werden darf. Für diesen Spezialfall konnte er eine Summe angeben, mit der sich die Bahnkurven der Objekte angeben lassen. 1889 sollte Poincarés Lösung gedruckt werden, ein paar Vorabveröffentlichungen waren schon an ausgewählte Fachleute verteilt worden. Doch plötzlich erkannte Poincaré einen gravierenden Fehler und rief Mittag-Leffler dazu auf, die Druckerpressen anzuhalten.

Die Reihe, die er gefunden hatte, konvergierte nicht. Das heißt, die Summe näherte sich nicht einer eindeutigen Funktion an, die der Bahnkurve eines Objekts entspricht. Um möglichen Konflikten mit dem König und anderen Fachleuten zu entgehen, beschloss Mittag-Leffler, Poincaré dennoch den Preis zu überreichen. Dieser sollte seine Arbeit jedoch nachbessern und für die bereits entstandenen Druckkosten aufkommen (diese beliefen sich auf 3500 Kronen, also 1000 mehr als das Preisgeld selbst). Als Poincaré seine Berechnungen durchging, erkannte er, was der Grund für die fehlende Konvergenz war: Die von ihm studierten Dreikörpersysteme verhielten sich chaotisch.

Das Chaos vermasselt alles

Das heißt nicht, dass die drei Massen keinen festen Regeln folgen. Sie unterliegen natürlich immer noch der Schwerkraft und folgen einer Bahnkurve, die sich aus der gegenseitigen Anziehung ergibt. Aber: Kleinste Änderungen am System können enorme Auswirkungen haben. »Kennt man die Bahnkurven eines Systems aus drei Sternen und verändert die Position des einen um nur wenige Millimeter, können die Flugbahnen plötzlich völlig verschieden verlaufen«, so der Mathematiker Richard Montgomery in einem Artikel für »Spektrum der Wissenschaft«, der an der University of California in Santa Cruz an diesem Thema forscht.

Betrachten wir zum Beispiel drei Körper, die wie in Eulers ursprünglicher Beschreibung stets eine gerade Linie bilden und sich so durch den Raum bewegen. Angenommen, man würde einen der Körper leicht verschieben, weil ein Asteroid darauf kracht. Das gesamte System würde infolgedessen plötzlich einer völlig anderen Dynamik folgen, die Massen würden wild durcheinandergeworfen – und letztlich würde vielleicht eine davon das System verlassen und in den Tiefen des Alls verschwinden. Mit der Erkenntnis, dass kleinste Veränderungen am System erhebliche Folgen haben können, gilt Poincaré als einer der Begründer der Chaostheorie. Und dieses Chaos ist in Liu Cixins Roman auch schuld daran, dass sich die Bewegungen der drei Sterne nicht exakt vorhersagen lassen – und warum die Trisolarier einen neuen Heimatplaneten brauchen.

Poincaré vermochte es mit seinem Ansatz also nicht, die von Mittag-Leffler gestellte Aufgabe zu lösen: eine konvergente Reihe für das Dreikörperproblem zu entwickeln. 1912 gelang dieses Meisterstück aber dem finnischen Mathematiker Karl Frithiof Sundman. Er lieferte eine unendliche Summe, die den Bahnkurven der Massen im allgemeinen Dreikörperproblem entspricht. Damit ist das Problem also gelöst, oder? Leider nicht ganz. Die Reihe konvergiert nämlich nur sehr langsam. Wie sich herausstellt, muss man etwa 10^8 000 000 (eine eins gefolgt von acht Millionen Nullen) Terme berechnen, bevor man ein verlässliches Ergebnis erhält. In der Praxis ist das Ergebnis folglich leider nutzlos.

Die Entwicklung von Computern eröffnete völlig neue Möglichkeiten, das Dreikörperproblem anzugehen. Fachleute konnten sich nun numerisch auf die Suche nach gebundenen Lösungen machen: Indem sie die Differenzialgleichungen näherungsweise mit Algorithmen lösten, erzielten sie erstaunliche Ergebnisse. So fand der Mathematiker Chris Moore im Jahr 1993 eine gebundene, stabile Lösung dreier gleicher Massen: Diese jagen einander entlang einer Kurve hinterher, die die Form einer 8 hat (oder eines Unendlichkeitssymbols).

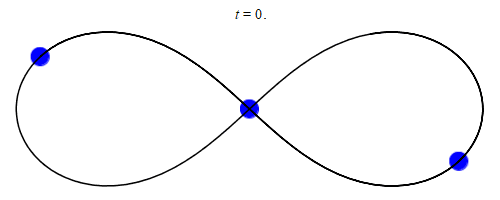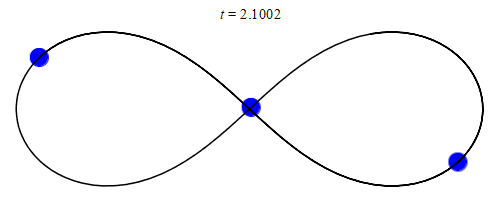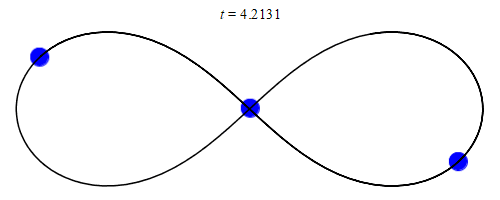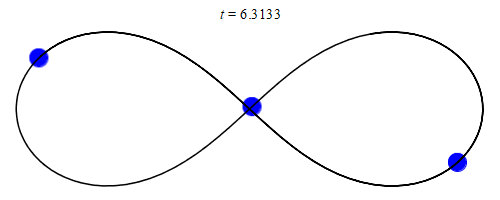
20 Jahre später fanden die Physiker Milovan Šuvakov und Veljko Dmitrašinović 13 weitere gebundene Lösungen des Dreikörperproblems, 2015 entdeckte Ana Hudomal 14 neue und drei Jahre später berechneten Xiaoming Li und Shijun Liao insgesamt knapp 2000 Lösungen. Die Bemühungen erreichten ihren bisherigen Höhepunkt im Jahr 2023, als Ivan Hristov, Radoslava Hristova, Dmitrašinović und Kiyotaka Tanikawa mehr als 12 000 neue Lösungen des Dreikörperproblems fanden, dank der Unterstützung von Supercomputern.

Welche Relevanz all diese Lösungen für reale Systeme haben, ist allerdings fraglich. Denn die Forscherinnen und Forscher haben bisher nicht belegen können, ob die Systeme stabil sind. Wenn wir hingegen im All auf Drei-Sterne-Systeme treffen, dann müssen diese stabilen Formen entsprechen, da sie sonst schnell wieder zerfallen würden. Aber wer weiß: Vielleicht beobachten wir schon bald eine achtförmige Bahnkurve dreier einander hinterherjagender Sterne. Ob ein Planet in einem solchen Sonnensystem lebensfreundliche Bedingungen entwickeln könnte, ist unklar. Doch anders als für die Trisolarier in Liu Cixins Roman ließe sich immerhin die Dynamik des Systems vorhersagen.