Schwarze Löcher -

Das dunkelste Geheimnis der Gravitation

• Einführung
• Historie Schwarzer Löcher
• Relativitätstheorie und Raumzeit
• Die Schwarzschild-Lösung
• Die Kerr-Lösung
• Eigenschaften Schwarzer Löcher
• Massenskala
• Akkretion - Materie am Abgrund
• Beobachtung Schwarzer Löcher
• Schwarze Löcher und Kosmologie
• Thermodynamik und Hawking-Strahlung
• Schwarze Löcher in Teilchenbeschleunigern
• Die Zukunft Schwarzer Löcher
• Literaturhinweise und Danksagungen

pdf (1.8 MB)

Die Kerr-Lösung

Erst 1963 folgte eine weitere wesentliche Lösung der Einsteinschen Gleichungen mit neuen physikalischen Eigenschaften: die Kerr-Lösung. Sie beschreibt rotierende, elektrisch ungeladene Schwarze Löcher und wurde von dem neuseeländischen Mathematiker Roy Patrick Kerr gefunden (Papier: Gravitational field of a spinning mass as an example of algebraically special metrics, 1963). Das Bild rechts zeigt Roy Kerr in den 1970er Jahren und zu seinem 70. Geburtstag am Kerr-Fest 2004 in Neuseeland (Fotos mit freundlicher Genehmigung von Roy Kerr).

Kerrs Raumzeit in der Astronomie

Die Kerr-Geometrie ist von unschätzbarem Wert für die moderne, relativistische Astrophysik. Die Rotation des Loches ist dabei nicht nur natürlich, sondern sogar notwendig. Denn nur mit dieser theoretischen, rotierenden Lösung der Einstein-Gleichungen sind viele Effekte in der Nähe von Schwarzen Löchern zu verstehen. Zu diesen Effekten gehören die magnetohydrodynamische Erzeugung von Jets, die Quasi-periodischen Oszillationen bei stellaren Schwarzen Löchern, die relativistische Verbreiterung von Emissionslinien, der Lense-Thirring-Effekt in Akkretionsscheiben, der Frame-Dragging-Effekt, der Blandford-Znajek-Mechanismus und Penrose-Prozesse.
Nicht nur die Theorie kann bislang nicht auf rotierende Schwarze Löcher verzichten. Der Clou ist, dass es mittlerweile den Astronomen gelungen ist, in einigen Fällen die Rotation eines kosmischen Schwarzen Loches nachzuweisen! Zu diesen Kandidaten eines Kerr-Lochs gehört das uns nächste, superschwere Schwarze Loch im Zentrum der Milchstraße und einige kleinere, stellare Schwarze Löcher in Röntgendoppelsternen.

Symmetrien des Kerr-Vakuums

Kommen wir nun zur Diskussion der Eigenschaften der Kerr-Lösung, die gelegentlich auch Kerr-Vakuum genannt wird, weil es eine Vakuum-Raumzeit ist. Sie weist zwei Symmetrien auf: die zeitliche Symmetrie heißt Stationarität und kann so verstanden werden, dass sich die Struktur der Raumzeit mit der Zeit nicht weiter entwickelt ('keine explizite Zeitabhängigkeit'). Dennoch rotiert die Raumzeit. Die räumliche Symmetrieeigenschaft ist eine Achsensymmetrie (Axialsymmetrie), also eine Symmetrie zu einer Achse wie bei einem Zylinder. Um diese Symmetrieachse rotiert das Loch.
Die Symmetrieeigenschaften kann man mathematisch aus der Killing-Gleichung dieser Metrik extrahieren. Sie führt gerade auf zwei so genannte Killing-Felder. Jedes dieser Felder kann mit einer Erhaltungsgröße in Verbindung gebracht werden: die Stationarität bedingt eine Erhaltung der Energie, die Axialsymmetrie bedingt die Erhaltung des Drehimpulses. Die Verknüpfung von Symmetrien mit Erhaltungsgrößen ist in der Physik gerade die Aussage des Noether-Theorems (benannt nach der Physikerin Emmy Noether).

Eine rotierende Raumzeit

Das Linienelement ist in der ART eine Gleichung, die alle Eigenschaften einer Raumzeit festlegt. Im Linienelement stecken alle Komponenten des metrischen Tensors, die bei der betreffenden Koordinatenwahl nicht verschwinden. Eine Raumzeit kann immer in unterschiedlichen Koordinaten dargestellt werden, die in unterschiedlicher Ausprägung ein direktes, intuitives Verständnis der Eigenschaften der Raumzeit erleichtern können. Auch die Komplexität mathematischer Rechnungen mit Raumzeiten hängt von dieser Koordinatenwahl ab. Generell gilt in der Physik: Je besser die Koordinaten an die Symmetrie des Problems (hier: der Raumzeit) angepasst sind, umso einfacher die mathematische Behandlung.

Das Linienelement der Kerr-Metrik (Gleichung rechts) ist komplizierter als im Schwarzschild-Fall und weist neue Kreuzterme auf. Mit Kreuztermen meint man Mischungen von Koordinaten in den metrischen Koeffizienten. Im Fall der Kerr-Lösung treten in Boyer-Lindquist-Koordinaten (einer Standardnotation der Kerr-Metrik) Mischungen zwischen der zeitlichen Komponente (t-Komponente) und der Azimutal-Komponente (Φ-Komponente) auf. Multipliziert man die Klammer im Linienelement aus, so findet man den Kreuzterm mit dΦ dt. Die Metrik geschrieben in Matrixform ist also nicht diagonal und weist von Null verschiedene Nebendiagonalelemente auf. Physikalisch ist das mit der rotierenden Raumzeit zu begründen. Die Kreuzterme mit zeitlichen Komponenten weisen darauf hin, dass die Metrik nicht statisch ist. Das ist schnell nachzuvollziehen, indem man gleichzeitig eine t- und eine Φ-Spiegelung durchführt: dann ist die Kerr-Geometrie unverändert (invariant). Es muss also zu einer drehenden Gravitationsquelle gehören!

Roy Kerr hat historisch die Metrik dieser rotierenden, ringförmigen Gravitationsquelle in pseudo-kartesischen Koordinaten formuliert. Weil diese der Axialsymmetrie nicht angepasst sind, sieht die Metrik dann deutlich komplizierter aus, wie die historische Form der Kerr-Lösung belegt. Allerdings kann man die Ringsingularität (dazu später) geeignet im pseudo-kartesischen System ableiten.

Boyer-Lindquist-Koordinaten - Die Standarddarstellung

Eine Standarddarstellung rotierender Schwarzer Löcher ist die Boyer-Lindquist-Form. Diese Koordinaten sind pseudo-sphärisch und der Symmetrie deutlich besser angepasst. In dieser Darstellung werden eine Reihe typischer Funktionen verwendet, die auch oben im Linienelement der Kerr-Geometrie zu finden sind. Diese Notation wurde Ende der 1960er Jahre gefunden (siehe Historie). Das radiale Verhalten der Boyer-Lindquist-Funktionen in der Äquatorialebene (der Poloidalwinkel θ ist π/2, also 90°) und im Falle eines maximal rotierenden Schwarzen Loches a = M zeigt das Diagramm oben. Auf der Symmetrieachse der rotierenden Raumzeit (dort gilt θ = 0) gibt es in Boyer-Lindquist-Form eine Koordinatensingularität. Eine weitere, schlimmere Koordinatensingularität gibt es am (äußeren) Ereignishorizont: Die Lapse-Funktion α und das Delta-Potential Δ werden beide am (inneren und äußeren) Horizont null. Das ist nämlich gerade die Definition eines Horizonts. Deshalb divergiert die Komponente g_rr des metrischen Tensors am Horizont. Beide Koordinatensingularitäten des Boyer-Lindquist-Koordinatensystems lassen sich beheben, wenn man Kerr-Schild-Koordinaten verwendet. Der metrische Tensor der Kerr-Geometrie in Kerr-Schild-Form weist zwar mehr nicht-verschwindende Komponenten (mehr Nebendiagonalelemente) auf, bleibt aber konvergent. Das wird im Wesentlichen durch die neue Funktion z gewährleistet, die die Kerr-Schild-Funktionen enthalten (Quelle: S.S. Komissarov 2004). Kerr-Schild-Koordinaten sind komplexer, aber nicht komplizierter, vor allem verhalten sie sich 'gutartig' an den Horizonten.

Im Schwarzschild-Fall koinzidiert der innere Horizont mit der zentralen Singularität bei r = 0. Bei maximaler Rotation eines Schwarzen Loches vom Kerr-Typ (a = -M oder a = M) koinzidieren innerer und äußerer Horizont und liegen bei einem Gravitationsradius. Das ist die bereits angesprochene, verbotene sichtbare Singularität. Für Zwischenwerte von a liegt der innere Horizont immer innerhalb des äußeren Horizonts.
Physikalisch bedeutet verschwindendes Delta-Potential, dass hier gerade die Rotverschiebung unendlich wird! (Hier nicht zu verwechseln mit der kosmologischen Rotverschiebung.) Strahlung aus diesem Bereich unterliegt dem Effekt der Gravitationsrotverschiebung und wird stark unterdrückt. Astronomisch macht sich diese Unterdrückung auf zweierlei Weise bemerkbar: Einerseits verliert die Strahlung Energie und wird röter; andererseits wird auch der Strahlungsfluss unterdrückt, d.h. weniger Strahlung (eine geringere Anzahl von Photonen) erreicht den Beobachter.

Im Schlepptau des rotierenden Lochs

Ein interessanter Umstand ist, dass das rotierende Schwarze Loch am Horizont alles, Materie, Licht, Magnetfelder, Beobachter etc. zwingt in seine Umlaufrichtung und mit gleicher Winkelgeschwindigkeit zu rotieren. Das verwundert nicht, denn das Loch ist die Raumzeit selbst, die rotiert. Dieses 'Mitschleppen von Objekten und des Bezugssystems' bezeichnen Relativitätstheoretiker mit dem englischen Fachbegriff frame dragging (engl. frame: Bezugssystem; to drag: ziehen). Es kann deshalb auch keine statischen Beobachter mehr nahe am Kerr-Loch geben. Das passende Beobachtersystem, das man dann in der Kerr-Metrik verwendet, nennt man den Bardeen-Beobachter oder das lokal nicht rotierende Bezugssystem (engl. locally non-rotating frame, LNRF) wie es James Bardeen selbst nannte. Heute sprechen die Experten meist vom ZAMO-System, für Zero Angular Momentum Observer. Dieser Beobachter rotiert mit der Raumzeit/mit dem Schwarzen Loch mit, deshalb verschwindet sein Drehimpuls (engl. angular momentum) lokal.
Das Symbol ω bei den Boyer-Lindquist-Funktionen bezeichnet die Frame-Dragging-Frequenz: Man erkennt, dass sie kurz vor dem Horizont stark ansteigt. Daran kann man sehen, dass die Rotation der Raumzeit im Bereich innerhalb der so genannten Ergosphäre wichtig und sehr hoch wird. Die Ergosphäre beginnt bei jedem Kerr-Loch in der Äquatorialebene bei einem Radius von r = 2M, also dem Schwarzschild-Radius. Ergoregion heißt der Bereich zwischen äußerem Horizont und Ergosphäre. Die Ergoregion ist eine an den Polen abgeplattete, sphäroide Region um den exakt kugelförmigen Horizont und markiert gerade die Grenze, ab der die raumzeitliche Rotation dominant wird. Mathematisch definiert man die Ergosphäre durch das Verschwinden der 00-Komponente (oder tt-Komponente) des metrischen Tensors. Die Zeitkoordinate t ändert an der Ergosphäre ihr Verhalten: Außerhalb ist sie zeitartig und innerhalb wird sie raumartig.

Der ZAMO rotiert nun aus dem Unendlichen betrachtet exakt mit dieser Winkelfrequenz ω. Sendet er einen Lichtblitz aus, propagiert ein Teil des Lichts in positive und der andere Teil in negative Richtung des Azimutwinkels Φ. Nur der ZAMO - und nur er - wird dann die getrennten Lichtblitze nach ihren Umläufen um das Loch exakt gleichzeitig bei sich empfangen. Andere Beobachter werden eine Verzögerung messen.

Dieselbe Diskussion kann man für den Schwarzschild-Fall (keine Rotation, a = 0) wiederholen. Die Abbildung oben zeigt, dass das Verhalten der einzelnen Funktionen sehr ähnlich ist, wie im Kerr-Fall, nur dass der Horizont nun doppelt so groß ist und bei r_H = 2 r_g, dem Schwarzschildradius, liegt. Die Funktionen ρ und ω mit Tilde (~) sind im Schwarzschild-Fall identisch und liegen aufeinander (blaue und gelbe Kurve). Es gibt jedoch eine wesentliche Ausnahme: das Drehimpulspotential ω bleibt konstant null, weil es proportional zu a ist. Das bedeutet, dass aufgrund des Frame-Dragging-Effekts jede Rotation am Horizont des Schwarzschild-Loches stoppen muss! Diese Bedingung wird rotierender Materie in einer Akkretionsscheibe durch die statische Raumzeit auferlegt. Man kann sie als Anti-Frame-Drag bezeichnen. Bei Computersimulationen von Akkretionsflüssen in Pseudo-Newtonschen Potentialen (Potentiale, die den relativistischen Schwarzschild-Fall nachahmen) muss diese Bedingung extra berücksichtigt werden. In voll relativistischen Simulationen ist sie hingegen automatisch enthalten.

Kerr-Löcher als Materieschleuder

Der Frame-Drag ist in der Magnetohydrodynamik (MHD) Schwarzer Löcher von besonderer Relevanz. Denn Magnetfelder in der Akkretionsscheibe werden durch frame dragging mitgezogen und verstärkt. Die Winkelfrequenz Ω, mit der die Raumzeit am Ereignishorizont r = r_H rotiert, ist gegeben durch die Gleichung rechts. Anschaulich werden global poloidale Magnetfelder in der Nähe von Kerr-Löchern verdrillt (Torsion). Die Feldlinien werden zusammengequetscht und in Rotation versetzt. Die Folge ist, dass die Magnetfeldstärke signifikant erhöht wird! Astrophysiker sprechen in diesem Zusammenhang vom ergosphärischen Dynamo, weil der magnetische Dynamo-Effekt in der Ergoregion eines rotierenden Loches stattfindet. Bei einem Schwarzschild-Loch funktioniert das nicht! Durch diesen Effekt werden bereits vorhandene Magnetfelder verstärkt und die Magnetfeldstruktur wird dominant toroidal ('schlauchartig'). Auch die Dynamik solcher Magnetfelder ist ein interessantes Studienobjekt, denn das rotierende Loch treibt eine Form magnetischer Wellen, also ein räumlich und zeitlich variables Magnetfeld. Diese so genannten Alfvén-Wellen pflanzen sich durch die Raumzeit fort. Die magnetische Struktur, die ein schnell rotierendes Loch nach außen treibt heißt torsionaler Alfvén-Wellenzug (engl. Torsional Alfvén Wave Train, TAWT). Es handelt sich um eine MHD-Welle, die sich etwa entlang der Rotationsachse des Schwarzen Loches bewegt und dabei Plasma mitreißt. Ihre Geschwindigkeit, die Alfvén-Geschwindigkeit, hängt von der Umgebungsdichte ab: In einem dichteren Medium wird diese MHD-Welle langsamer, in einem dünneren wird die magnetische Welle beschleunigt.
Der TAWT-Mechanismus ist ein sehr effizienter Vorgang, der Plasma aus der unmittelbaren Umgebung des Kerr-Loches nach außen befördert. Das funktioniert so effizient, dass der Ausfluss relativistische Geschwindigkeiten erreichen kann. In einigem Abstand können magnetische Nachbeschleunigungseffekte auftreten, die den Lorentz-Faktor signifikant steigern können (Das beobachten Astronomen auch in anderen Systemen - ohne Loch - in den Pulsarwinden, z.B. beim Crab-Pulsar.). Eine gute physikalische Größe, die diesen magnetisch getriebenen Ausfluss parametrisiert, ist der Poynting-Fluss. Dabei handelt es sich um einen elektromagnetischen Energiefluss, für den sowohl mit, als auch ohne Relativitätstheorie die mathematischen Ausdrücke beschafft werden können. Die im historischen Abriss angedeuteten MHD-Simulationen auf dem Hintergrund eines rotierenden Loches im Jahr 2002 wurden in der Folgezeit genauer analysiert. Dabei zeigte sich, dass ein trichterförmiger Ausfluss entlang der Rotationsachse des Loches nur dann effizient durch den Poynting-Fluss getrieben werden kann, wenn das Loch sehr schnell rotiert, a ~ 0.99 (Krolik et al. 2004 sowie spätere Arbeiten). Wir werden an diese Diskussion im nächsten Kapitel über Akkretion anknüpfen.

Soweit die Theorie - dass das etwas mit der Natur zu tun hat, belegt eindrucksvoll das Bild links. Es zeigt eine optische Fotografie der aktiven Galaxie M87 im Sternbild Virgo (dt. Jungfrau), aufgenommen mit dem Weltraumteleskop Hubble (Credit: AURA/STScI/NASA 2000). Die helle Punktquelle links oben ist der aktive Kern der Galaxie, wo Astronomen eine hohe, kompakte Masse von gewaltigen drei Milliarden Sonnenmassen nachgewiesen haben. Das wird als supermassereiches Schwarzes Loch interpretiert, das über Akkretion für die enorme Aktivität der Galaxie sorgt. Die Aktivität ist nicht nur an der gleißend hellen Punktquelle erkennbar; M87 erzeugt auch einen gigantischen Materiestrahl, der im Bild ebenfalls als bläulich-weißer Strahl zu sehen ist. Das ist ein spektakuläres Beispiel eines Jets, der aus einem Aktiven Galaktischen Kern (AGN) heraus geschossen wird. Die Astronomen kennen davon viele Beispiele, die sie in den unterschiedlichsten AGN-Typen, vor allem in Quasaren, Blazaren und Radiogalaxien beobachten. AGN-Jets sind großskalige Plasmaströme aus dem Herzen aktiver Galaxien. Sie erreichen unglaublich hohe Distanzen vom Kern und erstrecken sich dann bis auf die kpc- oder Mpc-Skala. D.h. das Plasma wird aus dem Kerngebiet bis Entfernungen von Millionen von Lichtjahren beschleunigt! (Zum Vergleich: Unsere Milchstraße hat einen Durchmesser von etwa 100000 Lichtjahren.)
Das im letzten Absatz beschriebene theoretische Szenario der magnetische getriebenen Jets favorisieren die Astrophysiker als Entstehungsmechanismus für relativistische AGN-Jets. Das bedeutet, dass das schnell rotierende supermassereiche Schwarze Loch, die Ursache für beinahe lichtschnelle Materieströme ist. Das heißt auch, dass der winzige Zentralbereich des AGN, nämlich die Ergoregion - die innersten zwei Gravitationsradien! - eine enorme Aktivität produzieren, die nicht nur weithin als kosmisches Leuchtfeuer zu sehen ist, sondern auch als gigantische, astronomisch beobachtbare Materiestrahlen zutage tritt.

Jets werden aber auch bei stellaren Quellen beobachtet und z.B. in abgeschwächter Form von Protosternen oder ebenfalls bei kompakten Objekten wie Weißen Zwergen, Neutronensternen oder stellaren Schwarzen Löchern in die Umgebung geschleudert. Ohne Schwarzes Loch ist die Physik der Jetentstehung eine andere (u.a. Blandford-Payne-Szenario) - wichtig ist in jedem Fall die Akkretion, weil sie die Materie zum Katapult befördert. Die Wechselwirkung von Akkretionsscheibe und kompakten Objekt treibt die Jets nach außen. Die Jets, die in der Umgebung Schwarzer Löcher erzeugt werden, sind besonders schnell - beinahe lichtschnell. Es sind relativistische Jets. Bei den extragalaktischen Makro-Jets der AGN und auch bei den Mikro-Jets von (stellaren) Mikroquasaren, Mikroblazaren und Gamma Ray Bursts (GRBs) werden relativistische Jets magnetisch getrieben! Wesentliche Zutaten für den Prozess sind eine schnell rotierende Raumzeit und Magnetfelder.

Welche Bedeutung haben Jets für den kosmischen Materiekreislauf? Jets reichern schließlich durch ihre Ausbreitung das interstellare und intergalaktische Medium mit Materie an und sorgen für eine kräftige Durchmischung. Somit sind Jets auf allen Längenskalen für eine gleichmäßige Verteilung der Metalle mit verantwortlich. Aus diesem 'Materialmix' können durch Gravitationskollapse (gravitative Instabilitäten) wieder neue Sterne höherer Metallizität entstehen. Jets spielen im 'kosmischen Recycling' eine wichtige Rolle bei der Durchmischung und Verteilung chemischer Elemente, die in der stellaren Nukleosynthese, Roter Riese und in Supernovae erzeugt werden. Und wer weiß: Vielleicht war die jetgetriebene Durchmischung auch eine Voraussetzung für die Entstehung des irdischen Lebens... Diese Hypothese rückt die Rolle Schwarzer Löcher in ein neues Licht. Schwarze Löcher sind keine fernen 'Materieschlucker', die uns egal sein können - sie haben etwas mit uns und unserem Dasein zu tun!

Bewegungen um den rotierenden Raumzeit-Schlund

Genauso wie die Planeten im Sonnensystem um die Sonne kreisen, gibt es auch stabile Keplerbahnen um ein Schwarzes Loch. Mit anderen Worten: Schwarze Löcher verschlingen nicht alles; wenn ein Körper genug Drehimpuls besitzt, kann er am dunklen Abgrund unbehelligt seine Kreise ziehen. Es gibt neben diesen stabilen Orbits aber auch instabile Bahnen. Im Prinzip gibt es fünf Möglichkeiten für die Bewegung eines Teilchens mit Drehimpuls in der Umgebung eines rotierenden Schwarzen Loches:

• i) Das Teilchen fällt direkt aus dem Unendlichen in das Schwarze Loch.
• ii) Das Teilchen wird aus dem Unendlichen eingefangen und fällt nach einigen Umläufen in das Schwarze Loch.
• iii) Das Teilchen beschreibt eine stabile Kreisbahn (mit konstantem Radius) um das Schwarze Loch.
• iv) Das Teilchen beschreibt eine elliptische Bahn mit einer Periastron-Drehung um das Schwarze Loch.
• v) Das Teilchen entkommt dem Schwarzen Loch, weil es genug Energie hat bzw. der Abstand ('Stoßparameter') sehr groß ist.

Diese Überlegungen macht man sich leicht am Potentialverlauf klar (wie im Lexikon bei der marginal stabilen Bahn diskutiert wird). Die Diskussion läuft analog zum Newtonschen Fall, nur dass man verallgemeinerte effektive Potentiale der Kerr-Geometrie benutzen muss. Analytisch behandeln Relativisten die Teilchenbewegungen (Materieteilchen oder Lichtteilchen - Unterschied: Ruhemasse) mit der Geodätengleichung. Eine Lösung dieser Gleichung auf der Kerr-Geometrie führt zu den Geodäten für Materieteilchen und den Nullgeodäten für Strahlung. Numerisch nutzen die Theoretiker dabei die Erhaltungsgrößen aus: neben den klassischen, konservativen Größen Masse, Energie und Drehimpuls existiert - und das nur ganz speziell in der Kerr Metrik! - eine vierte Erhaltungsgröße: die Carter-Konstante. Brandon Carter fand diese Größe 1968 (Papier: Global structure of the Kerr family of gravitational fields) aus der Separabilität der Hamilton-Jacobi-Gleichung. Die Carter-Konstante ist mit dem radialen und poloidalen Impuls (des Materie- oder Lichtteilchens ) assoziiert.

Licht in der Kerr-Metrik

Mit diesem Satz aus vier Erhaltungsgrößen lässt sich die Geodätengleichung sehr einfach integrieren. Die Geodätengleichung ist eine Differentialgleichung zweiter Ordnung, die nach dem Existenz- und Eindeutigkeitssatz eine eindeutige Lösung besitzt: die Bahn des Materieteilchens oder Photons. Die Simulationen mit Kerr-Ray-Tracern zeigen, dass die Lichtteilchen nicht nur durch den klassischen Doppler-Effekt, sondern auch durch relativistische Effekte stark beeinflusst werden. Diese vollkommen neuen Effekte heißen:

• Beaming - ein Effekt der Speziellen Relativitätstheorie - sorgt für eine Kollimation der Strahlung in Bewegungsrichtung des Emitters und für eine Blauverschiebung. Dieses Phänomen wurde auch in Teilchenbeschleunigern entdeckt, wo relativistische, geladene Teilchen eine scharf in Bewegungsrichtung gebündelte Strahlung abgeben: die Synchrotronstrahlung (benannt nach dem Typus des Teilchenbeschleunigers, einem Synchrotron ). In der Umgebung Schwarzer Löcher rotiert das Plasma außerhalb der marginal stabilen Bahn in der Regel Keplersch in einer geometrisch dünnen Standardakkretionsscheibe. Beaming bewirkt nun, dass der Teil der Scheibe, der auf den Beobachter zu rotiert heller wird, während der andere Teil der Scheibe, der vom Beobachter wegrotiert in der Helligkeit unterdrückt ('weggebeamt', aber nicht im Sinne von Scotty) wird.
• Gravitationsrotverschiebung sorgt vor allem nahe am Ereignishorizont für eine Verschiebung der Wellenlänge der Strahlung zum roten, niederenergetischen Ende hin. Auch der Strahlungsfluss, also die Intensität der Strahlungsquelle, wird unterdrückt. Ursache ist die starke Gravitation des Schwarzen Loches, gegen die die Photonen ankämpfen müssen. Um überhaupt dem Einflussbereich des Loches zu entkommen, verlieren die Photonen viel Energie. Dieser Effekt reduziert jede Emission am Horizont besonders stark! Man sagt: um das Schwarze Loch bildet sich ein 'Schatten' aus (wenn der Vergleich auch etwas hinkt). Eine angemessene Bezeichnung ist 'Dunkler Fleck'.

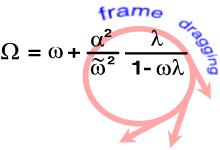Die Gleichung links zeigt, wie man allgemein relativistisch korrekt die Winkelgeschwindigkeit in der Kerr-Metrik berechnet. Dieser Ausdruck ist ganz fundamental und gilt immer in der Kerr-Geometrie. Man sieht die Abhängigkeit von den Boyer-Lindquist-Funktionen (ω mit ~ heißt 'Zylinderradius') und von dem Verhältnis der Erhaltungsgrößen Drehimpuls L und Energie E eines einfallenden Materieteilchens oder Photons, das in der Literatur häufig mit λ bezeichnet wird. Es ist der spezifische Drehimpuls des Teilchens. Die Winkelgeschwindigkeit wird am Horizont gerade ω, weil - wie aus dem Diagramm oben ersichtlich - α am Horizont null wird. Das ist gerade der bereits besprochene Frame-Dragging-Effekt: das Loch zwingt alles mit dem Horizont zu rotieren! Kurz notiert: Ω = ω.
Auf Keplerbahnen kann man für die Größen E und L (also auch λ) feststehende Ausdrücke ableiten, die nur von der Masse des Schwarzen Loches, dessen Rotationszustand (parametrisiert mit a) und dem Radius der Kreisbahn abhängen. Diese Ausdrücke gehen für große Radien in den Newtonschen Grenzfall über.
Man unterscheidet bei der Winkelgeschwindigkeit bzw. bei Kreisbahnen um ein Schwarzes Loch zwei Möglichkeiten: bei prograden Orbits rotiert das Teilchen (oder der Stern etc.) mit dem Schwarzen Loch in die gleichen Umlaufrichtung; bei retrograden Orbits entsprechend gegenläufig. Dies macht in den Gleichungen nur Vorzeichenunterschiede bei einigen Termen aus.
Stabile Kepler-Rotation auf Kreisbahnen ist nur bis zur marginal stabilen Bahn möglich. Dies gab gerade diesem charakteristischen Radius um ein Schwarzes Loch seinen Namen. Für kleinere Radien ist keine stabile Rotation mehr möglich und das Teilchen wird im freien Fall in das Schwarze Loch fallen, am Drehimpulswall reflektiert (wenn es genügend Drehimpuls hat) oder den Bereich des Schwarzen Loches wieder verlassen (wenn es genügend Energie hat).
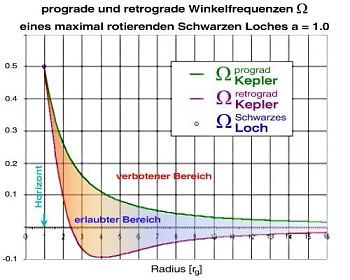Bis zur marginal stabilen Bahn kann man somit die Formel für Ω vereinfachen: Man erhält dann die bekannte Winkelfrequenz für Keplerbahnen. Alle Werte für die Winkelgeschwindigkeit, die überhaupt angenommen werden dürfen, liegen im farbigen Bereich der nächsten Abbildung: die obere Kurve ist gerade die prograde Winkelgeschwindigkeit, die untere Kurve die retrograde Winkelgeschwindigkeit. Der Bereich außerhalb dieser Kurven ist physikalisch verboten, weil hier das Geschwindigkeitsfeld nicht mehr global zeitartig ist.
Keplersche Rotation ist auf Basis der Gleichungen für die verschiedenen Radien an sich bis zum äußeren Horizont möglich, weil in den Extremfällen a = -M bzw. +M alle charakteristischen Radien bei M (erinnere G = c = 1) liegen: beide Horizonte, die marginal stabile Bahn, die marginal gebundene Bahn und der Photonenorbit fallen zusammen (nur die Ringsingularität bleibt im Zentrum des Lochs wie die Krümmungsinvarianten belegen). Doch muss dieser Extremfall unter besagten Einschränkungen des Kerr-Parameters gesehen werden. Vermutlich gibt es einen oberen Grenzwert für den Kerr-Parameter von etwa 0.99. Das Diagramm, das weiter unten folgt, zeigt die Abhängigkeit der charakteristischen Radien eines rotierenden Schwarzen Loches vom Kerr-Parameter.

Ringsingularität und Ergosphäre - Neue Strukturen in der Kerr-Lösung

Ein wesentlicher Unterschied zwischen rotierenden und nicht rotierenden Schwarzen Löchern ist, dass beim Kerr-Typus die intrinsische Punktsingularität durch die Ringsingularität in der Äquatorebene ersetzt wird. Die Auswertung der Krümmungsinvarianten wie dem Kretschmann-Skalar zeigt, dass die Krümmung der Raumzeit immer bei r = 0 divergiert, also unendlich wird. Die Krümmungssingularität bleibt am gleichen Ort, ändert aber ihren Typus. In der Kerr-Geometrie ist ein singulärer Massenstrom, der in einem unendlich dünnen Ring fließt, die Quelle des rotierenden Gravitationsfeldes. a nennt man den Rotations-, Spin- oder Kerr-Parameter, der den Drehimpuls des rotierenden Loches festlegt: a = 0 bedeutet keine Rotation (also Schwarzschild), a kleiner null (retrograd) bzw. a größer null (prograd) sind rotierende Kerr-Lösungen. Der Typus der Singularität folgt der globalen Symmetrie der Raumzeit: die kugelsymmetrische Schwarzschild-Metrik hat eine Punktsingularität, die achsensymmetrische Kerr-Metrik hat eine Ringsingularität.

Außerdem gibt es in der Kerr-Metrik ein abgeplattetes Gebiet, das man Ergosphäre nennt. Sie liegt dicht am äußeren Horizont und hat eine Berandung, die vom Poloidalwinkel abhängt: An den Polen des maximal rotierenden Kerr-Lochs fällt sie mit dem Horizont zusammen und steigt mit dem Kosinus des Poloidalwinkels bis auf 2 Gravitationsradien (also einem Schwarzschildradius) in der Äquatorebene an. Diese Begrenzung in der Äquatorebene ist unabhängig vom Rotationszustand des Schwarzen Loches und heißt statisches Limit: Im Schwarzschildfall gibt es keine Ergosphäre, denn hier fällt die Berandungsfläche mit dem Horizont zusammen. Akkretionsscheiben, die im Bereich zwischen ein und zwei Gravitationsradien existieren, nennt man ergosphärische Scheiben. Teilchen können in der Ergosphäre negative Energien annehmen. Auf diese Weise wäre es zumindest theoretisch möglich dem Schwarzen Loch Energie zu entziehen: Man schießt ein Teilchen in die Ergosphäre hinein, lässt es dort zerfallen. Nun muss man dafür sorgen, dass das Teilchen, das negative Energie trägt ins Loch fällt, während das andere die Ergosphäre wieder verlässt und aufgefangen wird. Auf diese Weise hätte man Energie aus dem Loch gewonnen. Diesen Mechanismus nennt man Penrose-Prozess. Die Astrophysiker stellen sich heute vor, dass die Makro-Jets Aktiver Galaktischer Kerne in der Ergosphäre Energie erhalten und so ein elektromagnetischer Energiefluss, Poynting-Fluss genannt, unmittelbar vor dem Horizont des rotierenden Schwarzen Loches getrieben wird, der den Jet nach außen elektromagnetisch beschleunigt. Die Astrophysiker sagen, dass relativistische Jets magnetisch getrieben sind (Details dazu auch in meiner Doktorarbeit).

Die Abbildung oben zeigt die Morphologie Schwarzer Löcher, hier der allgemeine Fall eines Kerr-Loches. Nähert man sich von außen diesem Objekt, so stößt man zunächst auf den Radius marginaler Stabilität (grüner Orbit). Dieser Abstand markiert den kleinstmöglichen Abstand, bei dem noch eine stabile Rotation um das Schwarze Loch möglich ist. Also gibt es für Radien kleiner als den für marginale Stabilität keine stabilen Kreisbahnen mehr. Kommt das Objekt näher heran, muss es entweder in das Schwarze Loch fallen oder auf einer ungebundenen Bahn verlassen.
Die marginal gebundene Bahn hingegen schließt sich weiter innen an (violetter Orbit). Dies ist der charakteristische Abstand, bei dem ein Testteilchen, das im Unendlichen ruhend erscheint, gerade an der Schwelle ist, um vom Schwarzen Loch angezogen zu werden.
Kurz vor dem (äußeren) Ereignishorizont, findet man die Photonensphäre (gelbe Kugelschale und Orbit): an diesem charakteristischen Radius können Photonen im Prinzip beliebig lange umlaufen, allerdings nur, wenn sie mit geeigneter Richtung auf diesen Orbit eingeschossen werden. Allerdings ist der Orbit instabil.
Dann schließt sich die oben beschriebene Ergosphäre an.
Die Morphologie ist im Wesentlichen für Kerr-Löcher mit a größer als 0.7 dieselbe, allerdings ragt der Photonenradius dann in die Ergosphäre hinein; ab a gleich 0.83 wandert auch der Radius für marginale Bindung in die Ergosphäre und schließlich ab einem Kerr-Parameter a von 0.94 auch der Radius für marginale Stabilität.

Sämtliche charakteristische Radien Schwarzer Löcher wurden in ihrer Abhängigkeit vom Kerr-Parameter a, der die Rotation des Schwarzen Loches parametrisiert, in der Abbildung oben dargestellt. Die Radien heißen:

• Radius marginaler Stabilität r_ms,
• Radius marginaler Bindung r_mb,
• Photonenradius r_ph,
• Radius der Ergosphäre r_erg (auch: statischen Grenze r_stat)
• äußerer Horizontradius r⁺_H,
• und innerer Horizontradius r^-_H.

Üblicherweise ist a eine positive Größe, dann spricht man von prograder Rotation, was bedeutet, dass der Drehsinn des rotierenden Schwarzen Loches mit einem umlaufenden Testteilchen oder z.B. der Akkretionsscheibe übereinstimmt. Dies entspricht also dem rechten Teil der Abbildung. Nimmt man hingegen für a negative Werte an, so handelt es sich um retrograde Rotation: Scheibe und Loch rotieren gegenläufig. Während Horizont, statisches Limit und auch die Ringsingularität unabhängig vom Vorzeichen von a sind (Symmetrie zur Vertikalen durch a = 0 in der Abbildung), hängen Radius marginaler Stabilität, Radius marginaler Bindung und Photonenradius stark vom Umlaufsinn ab. Retrograd ist demnach der Bereich links in der Abbildung. Besonders wichtig wird das beim Radius marginaler Stabilität, angewandt in der Akkretionstheorie, wo ein gegenläufig rotierendes Loch die Standardscheibe (die Keplerrotation bis r_ms aufweist) weit nach außen drückt: im Extremfall, a = -M, auf 9 Gravitationsradien!
Wie außerdem leicht zu erkennen ist, gilt immer, dass der Radius marginaler Stabilität außen liegt, sich dann der marginal gebundene Orbit und die Photonensphäre anschließen, bis schließlich der Ereignishorizont ganz innen liegt. Noch weiter innen, verhüllt vom inneren Horizont, dem Cauchy-Horizont, befindet sich die Ringsingularität.
Hier unterscheiden sich rotierende und nicht rotierende Schwarze Löcher eklatant, denn im Kerr-Fall wird die zentrale Punktsingularität zu einem (unendlich dünnen) Ring 'aufgeblasen'. Die Ringsingularität liegt in der Äquatorebene. Im Schwarzschild-Fall, a = 0, der genau in der Mitte der Abbildung liegt, kollabiert die Ringsingularität zu einer Punktsingularität, bleibt jedoch bei r = 0. Die intrinsischen Singularitäten der Schwarzen Löcher sind gerade die Quellen des Gravitationsfeldes der Vakuumlösungen der Einsteinschen Feldgleichungen.

Die maximal rotierenden Schwarzen Löcher, a = +M, haben die verblüffende Eigenschaft, dass alle charakteristischen Radien (bis auf den der Ergosphäre bzw. des statischen Limits) zusammenfallen, nämlich beim Radius r = 1 r_g! Aufgrund der kosmischen Zensur sind diese extremen Formen der Kerr-Lösung verboten. Wie die Abbildung zeigt, geht die gegenseitige Annäherung der charakteristischen Radien eines Kerr-Loches relativ glatt mit variablem Kerr-Parameter vonstatten (es gibt keine Sprünge/Unstetigkeiten der Radien als Funktion von a). Die Ergosphäre, also der Bereich negativer Energien, hat in diesem Fall (und ebenso für a = -M) ihr maximales Volumen, das Loch hingegen seinen kleinstmöglichen Radius des äußeren Horizonts. Dadurch dass Schwarze Löcher durch Akkretion schnell Drehimpuls gewinnen (engl. spin-up effect), ist zu erwarten, dass sehr viele von ihnen nahe an diesem Limit rotieren. Das legen auch aktuelle Computermodelle nahe (Volonteri et al. 2003; 2005). Rotation ist vital, um die Bildung von Poynting-Flüssen, die die Jets speisen, zu erklären.

Ein Plädoyer für Löcher ohne Ladung

Wie in der Historie Schwarzer Löcher bereits angemerkt, haben auch die Schwarzen Löcher der Kerr-Familie eine Verallgemeinerung erfahren: rotierende Schwarze Löcher mit elektrischer Ladung. Diese Kerr-Newman-Lösungen wurden 1965 von Newman et al. abgeleitet. Für Relativisten ist das Studium dieser Raumzeiten mit elektromagnetischen Feldern außerordentlich interessant. Für Astrophysiker spielt sie eher eine untergeordnete Rolle, weil die Ladung durch Akkretion von Plasma aus der Umgebung schnell kompensiert werden würde, sollte sich ein geladenes Schwarzes Loch gebildet haben. Aus diesem Grund betrachten Astrophysiker in der Regel nur ungeladene Schwarze Löcher vom Kerr-Typ.
Alle Versuche eine innere Kerr-Lösung als rotierendes Pendant zur inneren Schwarzschild-Lösung aufzufinden, sind bisher gescheitert! Eine gewisse Verwandtschaft zu diesen möglicherweise existierenden Lösungen weisen die Raumzeiten von Neutronensternen und Magnetaren auf: sie bestehen aus einem rotierenden, magnetisiertem Fluidum, das eine Kugel mit endlichem Radius ausfüllt. Bei diesen kompakten Objekten ist jedoch das Innere äußerst komplex aufgebaut, weil bei diesen hohen Materiedichten kernphysikalische Umwandlungsreaktionen einsetzen - es gibt bislang keine Einigkeit unter den Experten, welche Zustandsgleichung diese ultrakompakte Materie angemessen beschreibt. Es gibt also schon bei den 'Vorstufen eines Schwarzen Loches' Probleme. Ein vernünftiger Ansatz wäre es, den Übergang von einem Neutronenstern auf ein Schwarzes Loch konsistent zu rechnen - doch das bisher nicht gelungen.

pdf (1.8 MB)

Übersicht

© Andreas Müller, August 2007