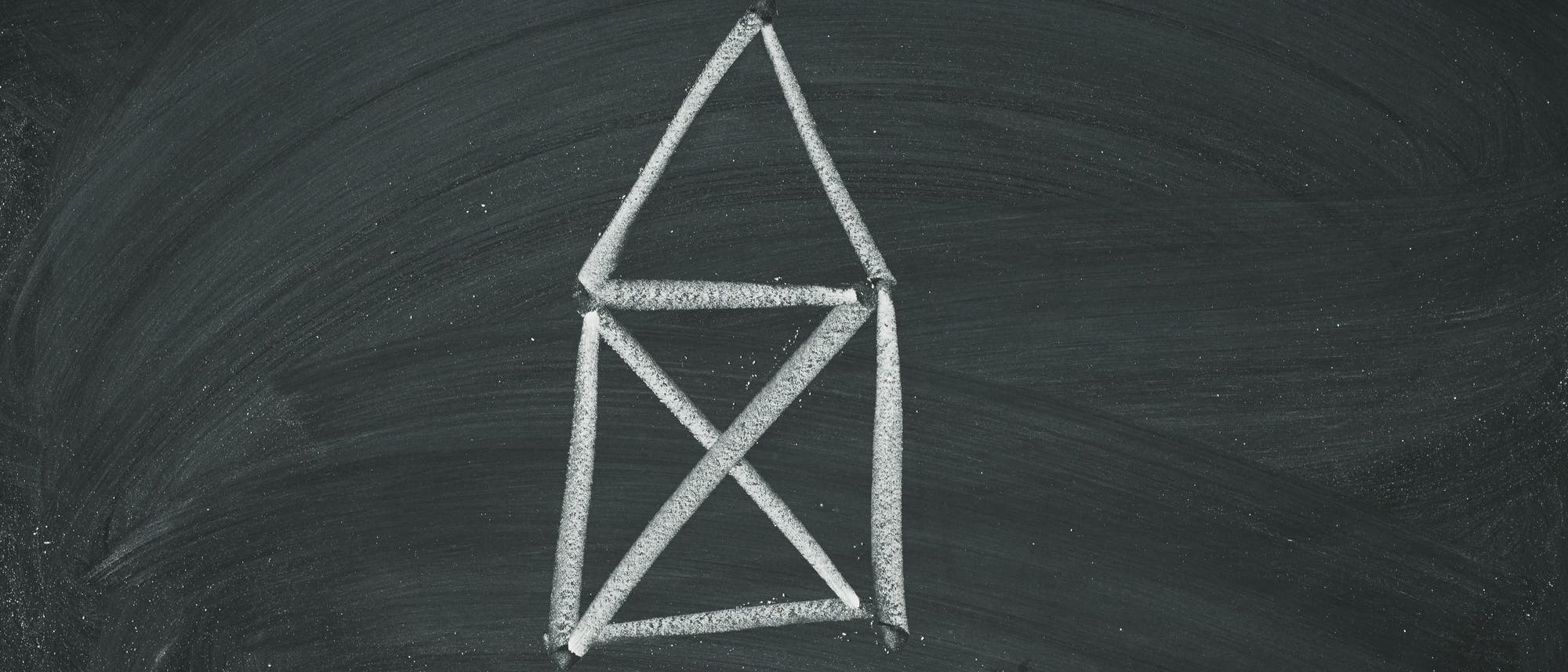
In der Sprache der mathematischen Disziplin der Graphentheorie kann man die Ausgangslage des Nikolaushauses so beschreiben:

G ist dabei ein »Graph«, also ganz allgemein eine abstrakte Struktur die aus Objekten und den Verbindungen zwischen den Objekten besteht, die »Knoten« und »Kanten« genannt werden. Der Graph besteht aus einer Knotenmenge V und einer Kantenmenge E, die in den letzten beiden Zeilen des Gleichungssystems angegeben sind. In diesem Fall hat der Graph fünf Knoten, also die vier Eckpunkte des Hauses und die Spitze des Daches. Die Menge der Kanten sind die Verbindungen zwischen den Knoten. Hier bezeichnen die Knoten ν₁ und ν₂ die beiden Punkte im Haus unten links und rechts; ν₃ liegt direkt über ν₂,ν₄ über ν₁ und ν₅ ist die Spitze des Daches. Für das fertige Nikolaushaus muss man zwischen diesen Punkten acht Linien ziehen, die in der Kantenmenge E angegeben sind.

Das klingt alles deutlich komplizierter als »Das ist das Haus vom Ni-ko-laus«. Aber mit der korrekten mathematischen Formulierung kann man aus dem Kinderspiel ein paar interessante Erkenntnisse rausholen. Zum Beispiel die Antwort auf die Frage, ob in diesem Graph ein Eulerweg oder gar ein Eulerkreis existiert.

Denn die zu lösende Aufgabe besteht ja darin, das gesamte Haus in einem durchgehenden Linienzug aus acht Strecken zu zeichnen. Also ohne den Stift abzusetzen und ohne eine Kante zweimal zu durchlaufen. In der mathematischen Sprache der Graphentheorie heißt so eine Abfolge von nacheinander durchlaufenden Linien »Kantenzug« und wird genau dann »Weg« genannt, wenn die Kanten alle unterschiedlich sind. Landet man am Ende des Weges wieder genau an dem Knoten, an dem man gestartet ist, dann erhält man einen »geschlossenen Weg« beziehungsweise einen »Kreis«.

Gerade Grade und der Eulerkreis

Den Zusatz »Euler« tragen die beiden Bezeichnungen oft, da sich der große Mathematiker Leonard Euler schon im frühen 18. Jahrhundert mit genau solchen Fragen beschäftigt hat. Damals ging es um die Suche nach einem Spazierweg durch Königsberg, der alle sieben Brücken genau einmal überquert und wieder am Ausgangspunkt endet. Euler zeigte, dass das nicht möglich ist, und so einen »Eulerkreis« können wir auch beim Haus des Nikolaus nicht finden.

Denn zwei der Knoten dort (Nummer 1 und 3) haben einen ungeraden »Grad«; von dort geht also eine ungerade Zahl an Kanten ab, während die restlichen Knoten alle einen geraden Grad haben. Will man das Haus aber in einem Zug zeichnen, jede Kante nur einmal durchlaufen und wieder am Ausgangspunkt landen, muss man den Stift natürlich in jeden Knoten ebenso oft hinein wie auch wieder hinaus führen. Das funktioniert nur, wenn alle Knoten einen geraden Grad haben.

Im Nikolaus-Graph existiert also kein Eulerkreis und einen Eulerweg – bei dem man nicht an den Ausgangspunkt zurückkehrt – kann man nur konstruieren, wenn man in einem der beiden Knoten mit ungeradem Grad startet, und am anderen ungeraden Knoten endet.

Wie beim echten Hausbau muss man also auch hier unten anfangen; ob man das aber links oder rechts tut, ist egal. Und auch dazwischen hat man noch einige Freiheiten. Beginnt man an Knoten 1, hat man insgesamt 44 unterschiedliche Möglichkeiten, den Regeln entsprechend zu zeichnen, und bei Knoten 2 zu enden (die gleichen 44 Möglichkeiten gibt es spiegelbildlich auch für den Start bei Knoten 2). Das sind deutlich mehr Möglichkeiten, die Aufgabe richtig zu lösen, als zu scheitern, denn das kann man nur auf zehn verschiedene Arten tun.

Wer also in der Vorweihnachtszeit Kinder für längere Zeit zu beschäftigen hat, kann sie nach einer kurzen Einführung in die Graphentheorie einfach mal all diese Varianten aufzeichnen lassen!