Lexikon der Mathematik: Das Collatz-Problem
G.J. Wirsching
Unter dem Collatz-Problem versteht man eine Frage zum Verhalten der Iterationen der Collatz-Funktion f : ℕ → ℕ,
\begin{eqnarray}f(n)=\left\{ {\begin{array}{c} n/2\,{\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{gerade n,}\\ 3n+1\,\,{\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{ungerade n.}\end{array} } \right.\end{eqnarray}
Es ist ziemlich sicher, daß diese Iteration zuerst von Collatz in den 1930er Jahren untersucht wurde, obwohl keine schriftlichen Quellen aus dieser Zeit vorliegen. 1985 publizierte der englische Mathematiklehrer Thwaites einen Artikel unter dem Titel „My Conjecture“, in dem er behauptet, er habe das 3n+ 1 Problem erfunden, und zwar am 21. Juli 1952 um vier Uhr nachmittags. Vermutlich als Antwort darauf publizierte Collatz 1986 in einem kleinen chinesischen Journal (und in chinesischer Sprache) einen Artikel, in dem er seine Entdeckung des 3n+1 Problem in die 1930er Jahre datiert und sehr plausibel beschreibt. Er schreibt, er habe nach Zusammenhängen zwischen elementarer Zahlentheorie und elementarer Graphentheorie gesucht. Einen solchen Zusammenhang stellte er dadurch her, daß er zu einer zahlentheoretischen Funktion f : ℕ → ℕ einen gerichteten Graphen Γf assoziierte, indem er ℕ als Knotenmenge nahm und jeweils von n nach f(n) einen Pfeil zog. Der Graph Γf wird heute Collatz-Graph zur Funktion f genannt. Z. B. ist der Collatz-Graph der Funktion g(n) = n+1 ein bei 1 beginnender unendlich langer Weg:
\begin{eqnarray}1\to 2\to 3\to 4\to 5\to 6\to 7\to \ldots \end{eqnarray}
Collatz suchte nun nach möglichst einfachen Funktionen f, deren Collatz-Graph einen Kreis enthält. Für ein solches f muß offenbar f (n) < n für manche n und f (n) >n für andere n gelten. Also wähle man f auf, sagen wir, den geraden Zahlen so, daß f (n) < n ist, und auf den ungeraden möge f (n) < n gelten. Z. B., für eine gegebene Zahl q ∈ ℕ:\begin{eqnarray}{f}_{q}(n)=\left\{ {\begin{array}{cc} n/2 & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{gerade n,}\\ qn+1 & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{ungerade n.}\end{array} } \right.\end{eqnarray}
In der mathematischen Forschungsliteratur findet das Collatz-Problem seit etwa 1972 Beachtung. 1985 erschien ein Überblicksartikel von J.C. Lagarias, der eine wahre Flut von bislang mehr als 100 Publikationen zum Collatz-Problem auslöste; siehe [1] für einen Überblick. Ein Beweis der 3n +1 Vermutung ist bisher (Ende 1999) noch nicht in Sicht, aber es gibt viele Teilresultate, die sich auf speziellere Fragestellungen oder auf Fragen über Verallgemeinerungen beziehen. Einige solcher Fragen sind:
- Gibt es noch andere Zykel? Wieviele, und welche?
- Endet jede f3-Trajektorie in einem Zykel, oder gibt es eine divergente Trajektorie?
- Von welchen Zahlen kann man beweisen, daß sie die 3n + 1 Vermutung erfüllen?
- Was passiert, wenn man 3n + 1 durch qn + 1 ersetzt?
- Gibt es noch andere interessante Verallgemeinerungen?
- Kann es sein, daß das Collatz-Problem nicht entscheidbar ist?
- Gibt es interessante Erweiterungen oder Umformulierungen des Collatz-Problems?
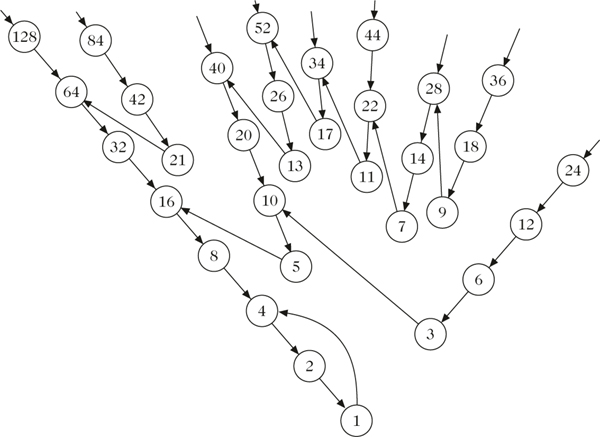
Ein Teil des Collatz-Graphen der Collatz-Funktion f3
Zur ersten Frage setzen wir zunächst die Collatz-Funktion f3 auf die ganzen Zahlen fort. Für negative Zahlen − n erhält man:
\begin{eqnarray}{f}_{3}(-n)=\left\{ {\begin{array}{cc} -n/2 & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{gerade n,}\\ -(3n-1) & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{ungerade n,}\end{array} } \right.\end{eqnarray}
\begin{eqnarray}{f}_{3}^{* }(n)=-{f}_{3}(-n)\end{eqnarray}
einen 3n − 1 Algorithmus. Nach einigem Probieren findet man für \({f}_{3}^{* }\) die Zykeln\begin{eqnarray}(1, 2),\quad (5, 14, 7, 20, 10), und
\begin{eqnarray}(17,50,25,74,37,110,55,164,82,41,122,61,182,91,272,136,68,34).\end{eqnarray}
Zum näheren Studium der Struktur möglicher Zykeln verändert man die Collatz-Funktion f3 zur sog. 3n + 1 Funktion T : ℤ → ℤ,
\begin{eqnarray}T(n)=\left\{ {\begin{array}{cc}{T}_{0}(n)=\displaystyle\frac{n}{2} & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{gerade n,}\\ {T}_{1}(n)=\displaystyle \frac{3n+1}{2} & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{ungerade n.}\end{array} } \right.\end{eqnarray}
Hierbei wird ausgenutzt, daß 3n + 1 für ungerades n stets gerade ist. Eine T-Trajektorie entsteht aus einer f3-Trajektorie dadurch, daß man in der letzteren jeweils die auf eine ungerade Zahl folgende Zahl wegläßt, z. B.:
\begin{eqnarray}\begin{array}{c}{f}_{3}:(27,82,41,124,62,31,94,47,142,\ldots )\\ T:(27,41,62,31,47,71,107,161,\ldots ).\end{array}\end{eqnarray}
Bei T-Trajektorien ist es möglich, daß auf eine ungerade Zahl wieder eine ungerade Zahl folgt, was bei f3-Trajektorien ausgeschlossen ist. Ein Kreislauf ist nun ein endliches Stück einer T-Trajektorie der Gestalt\begin{eqnarray}x\mathop{\to }\limits^{{T}_{1}}\ldots \mathop{\to }\limits^{{T}_{1}}y\mathop{\to }\limits^{{T}_{0}}\ldots \mathop{\to }\limits^{{T}_{0}}z,\end{eqnarray}
wobei zunächst ein Anstieg von x nach y in k Schritten der Form T1 erfolgt, und sich daran ein Abstieg von y nach z in ℓ Schritten des Typs T0 anschließt. Der Anstieg in k Schritten impliziert die Gleichung\begin{eqnarray}{2}^{k}(y+1)={3}^{k}(x+1),\end{eqnarray}
\begin{eqnarray}{2}^{l}z=y.\end{eqnarray}
Der bekannte T-Zykel (1, 2) ist ein Kreislauf mit den Schrittzahlen k = ℓ = 1. Da 2\begin{eqnarray}h=\displaystyle\frac{x+1}{{2}^{k}}=\displaystyle\frac{y+1}{{3}^{k}}\end{eqnarray}
eine ganze Zahl ist. Sucht man nach einem Kreislauf, der zugleich ein Zykel ist, so muß man x = z setzen, und dann folgt aus (5) und (6) die Gleichung\begin{eqnarray}y={2}^{l}x={2}^{l}({2}^{k}h-1),\end{eqnarray}
\begin{eqnarray}({2}^{k+l}-{3}^{k})h={2}^{l}-1.\end{eqnarray}
Umgekehrt liefert jede aus natürlichen Zahlen h, k, l bestehende Lösung von (7) einen Kreislauf, der zugleich ein Zykel ist. Nachdem Davison 1976 die Gleichung (7) hergeleitet hatte, präsentierte Steiner 1977 auf einer Tagung einen Beweis, daß h = k = l = 1 die einzige aus natürlichen Zahlen bestehende Lösung von (7) ist; Steiner’s Beweis beruht auf tiefliegenden Methoden der analytischen Zahlentheorie.Auf der Suche nach der Möglichkeit von T-Zykeln, die nicht notwendig ein Kreislauf sind, bewiesen Böhm und Sontacchi 1978 die folgende Zykelbedingung:
Sei x ∈ ℤ. Dann gibt es genau dann ein n ∈ ℕ mit T
\begin{eqnarray}({2}^{n}-{3}^{k})x=\displaystyle \sum _{j=0}^{k-1}{3}^{k-j-1}{2}^{vj}.\end{eqnarray}
Für festes k kann man (8) wieder als exponentiell diophantische Gleichung lesen, und mit Hilfe tiefliegender Resultate über Linearformen in Logarithmen konnten Belaga und Mignotte 1998 folgenden Satz beweisen:
Zu jeder natürlichen Zahl k gibt es nur endlich viele T-Zykel, in denen genau k Schritte des Typs T1vorkommen.
Dieser Satz gilt nicht nur für die 3n + 1 Funktion T, sondern auch für eine etwas allgemeinere Klasse von Funktionen.
Zur zweiten Frage, die als unabhängig von der ersten zu betrachten ist, ist ziemlich wenig bekannt. Man kann nicht von vorne herein ausschließen, daß es eine unbeschränkte (also divergente) f3-Trajektorie gibt, aber bewiesen ist das bis heute noch nicht. Andererseits gibt es durchaus Teilresultate.
Die Stoppzeit einer Startzahl x0 ist nach Terras wie folgt definiert:
\begin{eqnarray}\sigma ({x}_{0})=\min \{n \in {\mathbb{N}}:{T}^{n}({x}_{0}){x}_{0}\};\end{eqnarray}
gibt es in der T-Trajektorie mit Startzahl x0 keine Zahl kleiner x0, so setzt man σ(x0) = ∞. Angenommen, es gäbe eine divergente Trajektorie\begin{eqnarray}({x}_{0},{x}_{1},{x}_{2},\ldots )=({x}_{0},T({x}_{0}),{T}^{2}({x}_{0}),\ldots ),\end{eqnarray}
dann müßte diese unendlich viele Zahlen xn mit unendlicher Stoppzeit σ(xn) = ∞ enthalten: Zu jeder Schranke M gibt es einen größten Index n(M) derart, daß xn(M) ≤ M und xn >M für n >n(M). Das bedeutet, die T-Trajektorie mit Startzahl xn(M) ≤ M sinkt nicht mehr unter die Schranke M, also gilt σ(xn(M)) = ∞. Lagarias bewies 1985 folgendes Resultat über die Anzahlfunktion der Menge der Zahlen mit unendlicher Stoppzeit:Es gibt positive Konstanten c, γ mit γ< 1 und
\begin{eqnarray}|\{n\in {\mathbb{N}}:n\le x,\sigma (n)=\infty \}|\,\, \le \,\, c{x}^{\gamma }.\end{eqnarray}
Hieraus folgt, daß eine eventuell existierende divergente Trajektorie nicht „zu langsam“ gegen ∞ divergieren darf.
Die dritte Frage ist vielfach variiert und mit unterschiedlichen Methoden angegangen worden. 1976 bemerkte Terras, daß die Paritäten (gerade/ungerade) der ersten n Zahlen
\begin{eqnarray}{x}_{0}{x}_{1}=T({x}_{0}),\ldots,{x}_{n}-1\end{eqnarray}
einer T-Trajektorie nur von den letzten n Ziffern in der dyadischen Darstellung der Startzahl x0 abhängen, und daß diese Abhängigkeit sogar eineindeutig ist. Das kann man so deuten, daß der Anfang einer T-Trajektorie so etwas wie eine zufällige „Irrfahrt“ ist.Terras entwickelte einen auf der Binomialverteilung beruhenden Beweis folgenden Satzes:
Die Menge aller Startzahlen x0mit endlicher Stoppzeit hat die asymptotische Dichte 1.
Inzwischen gibt es eine ganze Reihe von sog. „Dichte 1“-Resultaten, die überwiegend als Verschärfungen dieses Satzes betrachtet werden können.
Diese „Dichte 1“-Resultate sind deutlich zu unterscheiden von Abschätzungen der Vorgängerdichte. Eine Zahl x ∈ ℕ heißt T-Vorgänger einer gegebenen Zahl a ∈ ℕ, wenn die T-Trajektorie mit Startzahl x die Zahl a enthält, wenn es also eine Schrittzahl n ≥ 0 gibt mit T
\begin{eqnarray}\mathcal{P}(a)=\{x\in {\mathbb{N}}:{T}^{n}(x)=a\, {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{ein n} \ge 0\}.\end{eqnarray}
\begin{eqnarray}Z_a (x) = \left| {\left\{ {n \in P(a):n \leqslant x} \right\}} \right|,\end{eqnarray}
ist das Collatz-Problem äquivalent zur Behauptung\begin{eqnarray}\begin{array}{cc}{Z}_{1}(x)=x & {\rm{f}\rm{\ddot{u}}\rm{r}}\,\text{alle}\, x \in {\mathbb{N}}\end{array}.\end{eqnarray}
Es gibt nun schon eine Reihe von unteren Abschätzungen der Form\begin{eqnarray}\begin{array}{cc}{Z}_{1}(x)\gt {x}^{\beta } & {\rm{f}\rm{\ddot{u}}\rm{r}}\,{\rm{gen}\rm{\ddot{u}}\rm{gend}}\,\text{gro}\unicode{x00DF}e\,x\in {\mathbb{N}}\end{array},\end{eqnarray}
\begin{eqnarray}\mathop{\mathrm{lim}\inf }\limits_{x\to \infty }\,\displaystyle\frac{{Z}_{a}(x)}{x}\gt 0\quad{\rm{f}\rm{\ddot{u}}\rm{r}}\quad a\rlap{/}{\equiv }0\,\mathrm{mod}\,3,\end{eqnarray}
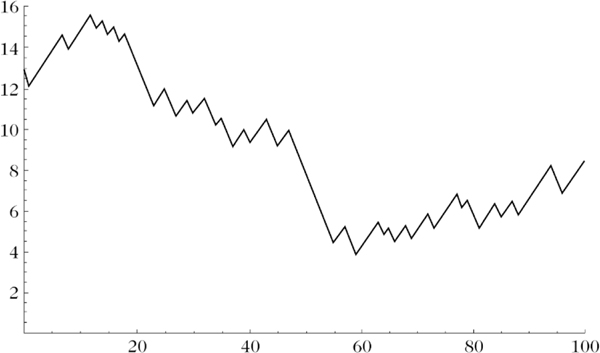
die man auch als positive-Dichte-Vermutung bezeichnet [1].Die ersten 100 Schritte einer typischen T-Trajektorie; nach rechts ist die Schrittnummer n abgetragen, nach oben die n-te Iterierte T
Zur vierten Frage: Ersetzt man die Collatz-Funktion f3 durch eine wie in (2) definierte Funktion fq, so kann man analog zum Collatz-Problem die Frage stellen, ob jede fq-Trajektorie die 1 enthält. Für q > 3 ist das i. allg. falsch: Franco und Pomerance nannten 1995 eine ungerade Zahl Crandall-Zahl, wenn es eine Startzahl x0 ∈ ℕ gibt, deren fq-Trajektorie die 1 nicht enthält. Sie bewiesen, daß jede Wieferich-Zahl eine Crandall-Zahl ist, und daß die Menge der Wieferich-Zahlen in den ungeraden Zahlen die relative asymptotische Dichte 1 hat. Das bedeutet, daß für „fast alle“ ungeraden Zahlen q > 3 eine qn + 1 Vermutung falsch ist.
Umfangreiche Computerexperimente, die von Matthews in Brisbane durchgeführt wurden, legen es nahe, daß ein qn+1 Algorithmus mit einer ungeraden Zahl q ≥ 5 schnell wachsende Trajektorien hat. Aber bisher gibt es noch für kein einziges q einen mathematischen Beweis dafür, daß der qn+1 Algorithmus tatsächlich eine divergente Trajektorie besitzt.
Ein anderer Typ von Verallgemeinerungen, der studiert wurde, sind die Hasse-Funktionen. Zur Konstruktion einer Hasse-Funktion benötigt man zwei teilerfremde natürliche Zahlen d, m mit d ≥ 2, und ein vollständiges Restsystem modulo d,
\begin{eqnarray}{A}_{d}=\{0,{r}_{1},\ldots,{r}_{d-1}\},\end{eqnarray}
mit der natürlichen Projektion φ : ℤ → Ad, die durch \(\phi (x)\equiv x\,\, \mathrm{mod}\,d\) gegeben ist. Die Hasse-Funktion H : ℤ → ℤ ist dann definiert durch\begin{eqnarray}H(x)=\left\{ {\begin{array}{cc}\displaystyle\frac{x}{d} & \text{falls}\,d|x,\\ \displaystyle \frac{mx-\phi (mx)}{d} & \text{sonst.}\end{array} } \right.\end{eqnarray}
Die in (3) definierte 3n + 1 Funktion T ist eine Hasse-Funktion mit d = 2, m = 3 und A2 = {0,1}. Möller bewies 1978 ein „Dichte 1“-Resultat für Hasse-Funktionen unter der zusätzlichen Bedingung m< d
Eine weitergehende Verallgemeinerung ist die auf periodisch-lineare Funktionen, die wie folgt definiert sind. Seien p ≥ 2 eine ganze Zahl, und a0, …, ap−1, b0, …, bp−1 rationale Zahlen, die den 2p Bedingungen
\begin{eqnarray}{a}_{k}p,\,{a}_{k}k+{b}_{k}\in {\mathbb{Z}}\,\,{\rm{f}\rm{\ddot{u}}\rm{r}}\,k=0,\ldots p-1,\end{eqnarray}
\begin{eqnarray}U(n)={a}_{k}n+{b}_{k}\,\,{\rm{f}\rm{\ddot{u}}\rm{r}}\,\,n=k\,\mathrm{mod}\,p\end{eqnarray}
definierte Funktion ganze Zahlen auf ganze Zahlen ab; ein solches U nennt man periodisch-lineare Funktion. Die 3n+1 Funktion T ist eine periodischlineare Funktion mit \(p=2,{a}_{0}=\displaystyle\frac{1}{2},{a}_{1}=\displaystyle\frac{3}{2},{b}_{0}=0\,\,\text{und}\,{b}_{1}\frac{1}{2}.\)Conway konstruierte 1972 eine periodischlineare Funktion g mit der Eigenschaft, daß das Grenzverhalten der g-Trajektorien das Halteproblem von Turing-Maschinen codiert. Daraus folgt, daß das Grenzverhalten der g-Trajektorien algorithmisch nicht entscheidbar ist; das ist ein Teilresultat zur sechsten Frage. Man kann aus Conways Resultat aber keine Informationen über die algorithmische Entscheidbarkeit des Grenzverhaltens der 3n+1 Trajektorien herleiten. Im Gegensatz zur 3n + 1 Funktion hat die von Conway konstruierte periodisch-lineare Funktion g die spezielle Eigenschaft bk = 0 für jedes k = 0, …, p − 1.
Zur siebten Frage ist anzumerken, daß es Umformulierungen und Erweiterungen des Collatz-Problems in ganz verschiedene mathematische Kontexte gibt. Zunächst einmal ist die 3n +1 Funktion T durch (3) ganz offensichtlich auf der Menge ℤ2 der 2-adischen Zahlen definiert, also auf den unendlichen Folgen (a0, a1, …) mit aj ∈ {0, 1}, die man gewöhnlich in Form der (in der 2-adischen Metrik konvergenten) Reihe
\begin{eqnarray}a={a}_{0}+{a}_{1}\cdot 2+{a}_{2}\cdot {2}^{2}+\ldots =\displaystyle \sum _{j=0}^{\infty }{a}_{j}{2}^{j}\end{eqnarray}
schreibt; hierbei heißt a ∈ ℤ2 gerade, wenn a0 = 0, und ungerade, wenn a0 = 1 ist. Aus Resultaten von Matthews und Watts (1984) und Müller (1991) gewinnt man folgende Informationen über die Funktion T:Die Funktion T : ℤ2 → ℤ2ist surjektiv, nicht injektiv, unendlich oft differenzierbar, nicht analytisch, sie erhält das Haar-Maß auf ℤ2, und sie ist stark mischend.
Wählt man für jedes j ≥ 0 die Ziffer aj derart, daß
\begin{eqnarray}{T}^{j}(a)\equiv {a}_{j}\,\mathrm{mod}\,2\end{eqnarray}
gilt, daß also aj die Parität der j-ten Iterierten T\begin{eqnarray}{Q}_{\infty }:{{\mathbb{Z}}}_{2}\to {{\mathbb{Z}}}_{2},\end{eqnarray}
die nach den Resultaten von Terras stetig und bijektiv ist und das Haarsche Maß auf ℤ2 erhält. Müller bewies 1994, daß Q∞ nirgends differenzierbar ist; unabhängig hiervon zeigte Bernstein 1994, daß die von ihm explizit konstruierte Umkehrfunktion \(\Phi ={Q}_{\infty }^{-1}\) nirgends differenzierbar ist. In diesem Kontext ist die 3n + 1 Vermutung äquivalent zur Behauptung\begin{eqnarray}{Q}_{\infty }({\mathbb{N}})\subset \displaystyle\frac{1}{3}{\mathbb{Z}}.\end{eqnarray}
Eine Umformulierung in das Reich der holomorphen Funktionen auf der komplexen Einheitskreisscheibe ist durch folgenden Satz von Berg und Meinardus (1994) gegeben:
Die 3n + 1 Vermutung ist genau dann richtig, wenn die Funktional-Gleichung
\begin{eqnarray}h({z}^{3})=h({z}^{6})+\displaystyle\frac{1}{3z}\displaystyle \sum _{j=0}^{2}{\zeta }^{j}h({\zeta }^{j}{z}^{2}),\end{eqnarray}
\begin{eqnarray}h(z)={h}_{0}+\displaystyle\frac{{h}_{1}z}{1-z}\end{eqnarray}
mit beliebigen Konstanten h0, h1 ∈ ℂ besitzt.Chamberland formulierte 1996 das Collatz-Problem als ein Problem der Dynamik analytischer Funktionen: Er entdeckte, daß die durch die Gleichung
\begin{eqnarray}{g}_{0}(x)=x+\displaystyle\frac{1}{4}-\displaystyle\frac{2x+1}{4}\cos (\pi x)\end{eqnarray}
\begin{eqnarray}{g}_{0}(x)=T(x)\,\,{\rm{f}\rm{\ddot{u}}\rm{r}}\,x\in {\mathbb{Z}}\text{.}\end{eqnarray}
Chamberland’s Funktion g0 hat die etwas störende Eigenschaft, daß die kritischen Punkte von g0 nicht genau bei den ganzen Zahlen liegen.1998 bestimmten Letherman, Schleicher und Wood alle ganzen Funktionen g : ℂ → ℂ, die einerseits die 3n+1 Funktion T fortsetzen und andererseits die Eigenschaft haben, daß alle ganzen Zahlen kritische Punkte von g sind. Dadurch gelang esihnen, das Collatz-Problem in die schon gut entwickelte Terminologie der holomorphen Dynamik zu übersetzen. Allerdings mußten sie feststellen, daß damit das Wesentliche des Collatz-Poblems nicht leicht zu fassen ist: Jede andere qn+1 Funktion läßt sich nämlich in ähnlicher Weise fortsetzen, und es scheint schwierig, einen Unterschied in der holomorphen Dynamik auszumachen.
Zum Abschluß bleibt noch zu erwähnen, daß das Collatz-Problem eine ganz praktische Anwendung hat. Einige Fragen zur 3n + 1 Dynamik, z. B. die Suche nach Startzahlen mit besonders großer Stoppzeit, können mit einem gut programmierten Computer angegangen werden. Das hat mehrere Autoren (z. B. Leavens und Vermeulen 1989 und 1992, später Roosendaal und andere) dazu veranlaßt, die 3n + 1 Iterationen dazu zu benutzen, Unterschiede zwischen verschiedenen Programmiersprachen und Programmiertechniken zu messen, oder die Qualität neu entwickelter Programmiersysteme zu untersuchen.
Literatur
[1] Wirsching, G. J.: The Dynamical System Generated by the 3n + 1 Function. Springer Berlin, 1998.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.