Hemmes mathematische Rätsel: Die Dreiecke im Quadrat
Der amerikanische Software-Ingenieur Wei-Hwa Huang wurde 1975 geboren und ist Mitglied des US-Teams der World Puzzle Federation. Mit achtzehn Jahren gewann er die Putnam Competition, einen amerikanischen Mathematikwettbewerb für Studenten. In den Jahre 1995, 1997, 1998 und 1999 gewann er die World Puzzle Championship, eine internationale Puzzlemeisterschaft, die jedes Jahr in einem anderen Land ausgetragen wird. Im vorletzten Jahr wurde er amerikanischer Sudoku-Meister. Huang löst nicht nur Rätsel und Puzzle, sondern erfindet auch welche. Gemeinsam mit Thomas Snyder hat er die beiden Sudoku-Bücher »Mutant Sudoku« und »Sudoku Masterpieces« und mit Jerry Slocum und Dieter Gebhardt das Zauberwürfelbuch »The Cube: The Ultimate Guide to the World's Bestselling Puzzle« geschrieben. Im Jahr 2009 veröffentliche er in Dick Hess’ Buch »All-Star Mathlete Puzzles« das folgende kleine geometrische Problem:
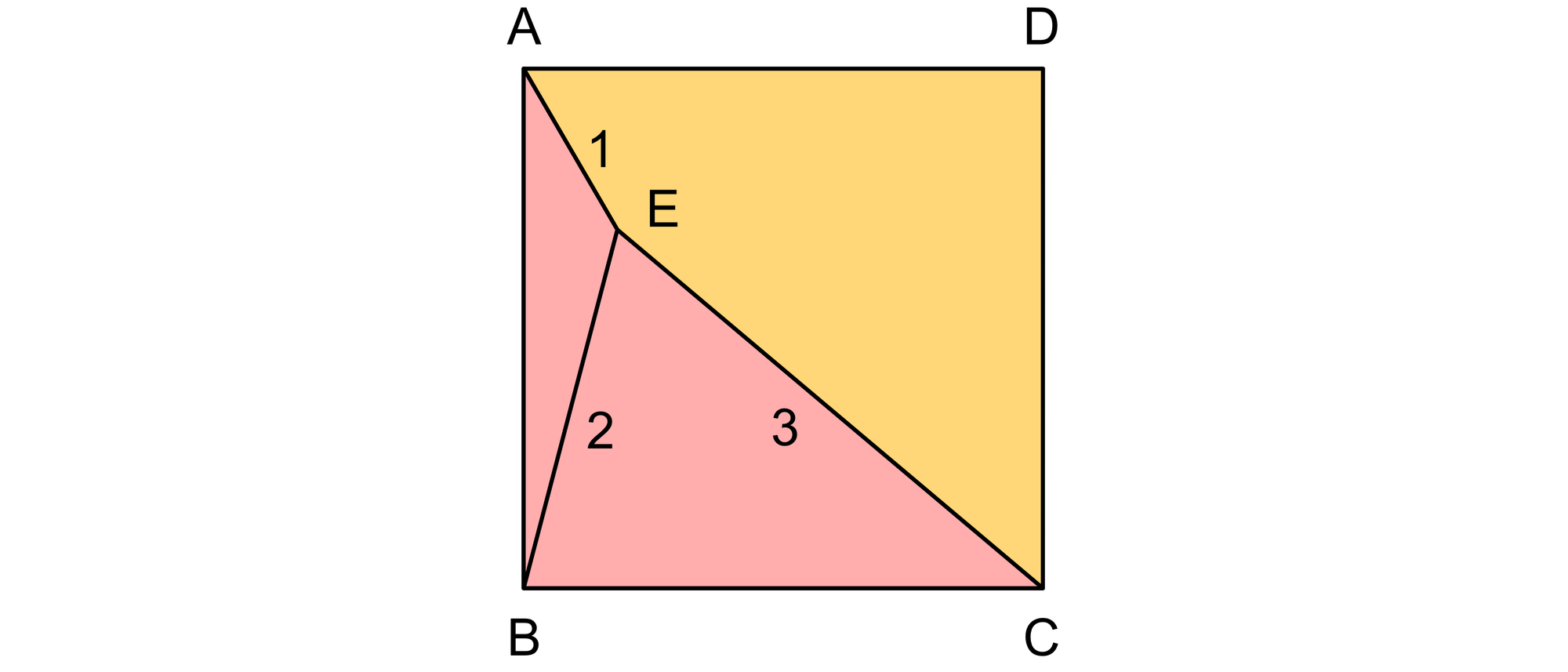
Im Inneren eines Quadrates ABCD liegt der Punkt E. Die Verbindungsstrecken von diesem Punkt E zu den Ecken A, B und C haben die Längen 1, 2 und 3. Wie groß ist rosa Fläche des Quadrats?
Dreht man das Dreieck BCE gegen den Uhrzeigersinn um 90 Grad um die Ecke B, so fällt C mit A zusammen und E wird zu E’. Folglich hat das Dreieck E’BE bei B einen rechten Winkel. Der Flächeninhalt eines rechtwinkligen Dreiecks ist das halbe Produkt seiner beiden Kathetenlängen. Darum hat das Dreieck E’BE die Fläche 2.
Mit dem Satz des Pythagoras lässt sich sein Hypotenusenquadrat zu (E’E)2 = 8 und damit seine Hypotenuse zu E’E = √8 = 2√2 berechnen. Da 8 + 12 = 32 ist, muss nach dem Satz des Pythagoras auch das Dreieck E’EA rechtwinklig sein, wobei der rechte Winkel bei E liegt.
Somit hat das Dreieck E’EA einen Flächeninhalt von √2. Die rosa Fläche in dem Quadrat hat folglich einen Inhalt von 2 + √2 ≈ 3,4142.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.