Mandelbrots Apfelmännchen
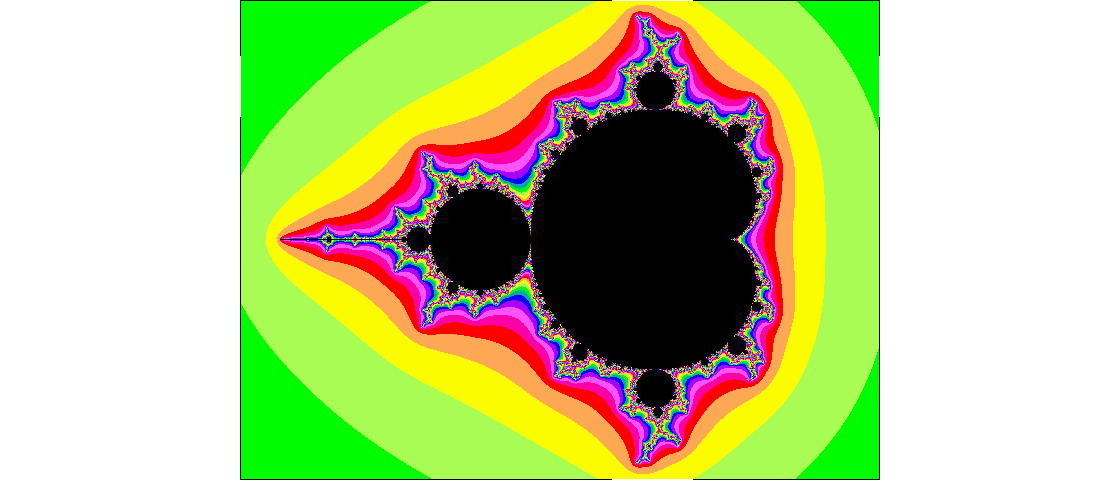
Wissen Sie, nach welcher Rechenvorschrift das Apfelmännchen gezeichnet wird? Und wenn Sie es wissen, können Sie es ohne höhere Mathematik erklären?
Man nimmt eine Ebene und wählt zwei bevorzugte Punkte \(O\) und \(E\) aus. Dann geht man der Reihe nach "alle" Punkte der Ebene durch (bis zum Abstand 2\(OE\) von \(O\)) und wendet auf jeden von ihnen die folgende Prozedur an:
- Der Punkt bekommt den Namen \(P\). Konstruiere einen weiteren Punkt \(P'\) wie folgt: Wende auf das Dreieck \(OEP\) eine Drehstreckung an derart, dass das Bild der Seite \(OE\) mit \(OP\) zusammenfällt. \(P'\) ist dann der Bildpunkt von \(P\). Die Seiten des Dreiecks \(OPP'\) sind also um den Faktor \(OP/OE\) größer als die von \(OEP\) und um den Winkel \(POE\) weiter von \(OE\) weggedreht.
- Füge dann an den neuen Punkt \(P'\) einen Pfeil \(OP\) (mit gleicher Länge und in dieselbe Richtung zeigend) an. Dessen Spitze ist der neue Punkt \(P_1\).
- Bilde nun \(OP_1\) durch Drehstreckung um dem Winkel \(EOP_1\) mit dem Verhältnis \(OP_1/OE\) nach \(OP'_1\) ab und addiere wieder den Pfeil \(OP\), mit dem Ergebnis \(P_2\). Wiederhole diese Aktion, d. h. die Drehstreckung mit dem jeweiligen Zwischenergebnis und die Pfeil-Addition mit immer dem gleichen Pfeil \(OE\), ziemlich oft. Das ist eine richtige Aufgabe für einen Computer.
Es können nun drei verschiedene Dinge geschehen:
- Die Punkte \(P_i\) streben immer genauer einem festen Punkt zu (Konvergenz);
- die Punkte \(P_i\) springen zwischen mehreren Gegenden hin und her und nähern sich dabei immer genauer abwechselnd bestimmten Punkten (zyklisches Verhalten);
- der Abstand \(OP_i\) wächst über alle Schranken hinaus.
Wenn festgestellt ist, wie es mit einem bestimmten Punkt \(P\) ausgeht, malen wir ihn mit einer entsprechenden Farbe an.
Man nennt die Menge aller Punkte, auf die (1) oder (2) zutrifft, die Mandelbrot-Menge (nach Benoît Mandelbrot). Im Bild der Frage ist sie wie in vielen Darstellungen schwarz gefärbt. Die bunten Bereiche um sie herum zeigen dann abgestuft an, mit wie vielen oder wenigen Schritten bestimmte große Entfernungen übertroffen werden, also sozusagen das Tempo des divergenten Verhaltens.
Interessanter (wenn auch etwas kniffliger und/oder langwieriger zu bestimmen) ist die Frage, ob ein Punkt zum Konvergenzbereich gehört oder im Falle des zyklischen Verhaltens zu welcher Zyklus-Zahl. Das folgende Bild zeigt dieses:
Die Punkte mit den Koordinaten (0;0) bzw. (1;0) sind unsere festen Punkte \(O\) und \(E\). Zyklus 1 bedeutet natürlich Konvergenz, die Figur erinnert an einen Apfel und ist exakt eine Hypozykloide. Die anderen gefärbten Flächen sind Kreise, die den Apfel bzw. einander paarweise berühren und dabei unendlich weit verzweigte Verästelungen aus immer kleineren Kreisen bilden (das ist eine fraktale Struktur!). Das ist aber hier leider nicht besonders gut zu sehen. Jede Verästelung von innen nach außen bedeutet eine Vervielfachung der Zykluszahl um einen ganzzahligen Faktor. Die Potenzen von 2 treten links (der Reihe nach) auf, an die Ärmchen mit der 3 grenzen nicht nur die 6, sondern auch 9 und 12 usw. (leider zu klein, um hier sichtbar zu sein).
Greift man einen beliebigen Punkt aus dem Bild heraus und wiederholt die zuvor vorgegebenen Schritte mit lauter verschiedenen Startpunkten (nicht nur mit \(P\)), so kann man auch die Ebene der Startpunkte färben. Die Menge der Punkte mit konvergentem oder zyklischem Verhalten wird dann nach Gaston Julia benannt. Zu jedem Punkt aus dem Mandelbrot-Bild gibt es ein Julia-Bild, wobei interessanterweise die Verästelungsstruktur des jeweiligen Julia-Bildes mit der zugehörigen Stelle im Mandelbrot-Bild übereinstimmt. Das Bild zeigt zahlreiche Julia-Mengen in sehr kleinem Maßstab, jede an der richtigen Stelle der Mandelbrot-Menge.
Wenn Ihnen komplexe Zahlen vertraut sind, haben Sie die Drehstreckung sicher als Quadrierung wiedererkannt: Man kann die Rechenvorschrift als \(z \to z^2+c\) mit dem Start bei \(z=0\) und einer komplexen Zahl \(c\) für jeden zu färbenden Punkt formulieren.
Wenn man die gleiche Rechnung mit reellem \(c\) macht, wird das zugehörige Bild nach Feigenbaum benannt.
Hier noch zwei Ausschnitts-Vergrößerungen aus dem Mandelbrot-Bild:
Schreiben Sie uns!
Beitrag schreiben