Charles Wilderman Trigg wurde 1898 in Baltimore (USA) geboren. Er arbeitete zunächst als Chemiker, Ingenieur und Mathematiker in der Industrie und von 1950 bis 1963 als Professor an der University of Southern California in Los Angeles. Er starb 1986. Trigg gehörte zu den kreativsten Erfindern von mathematischen Problemen und Denksportaufgaben des 20. Jahrhunderts. Niemand kennt die Anzahl der von ihm in Zeitschriften veröffentlichten Aufgaben genau, aber es werden vermutlich Zehntausende sein. Trigg hat jedoch nur ein einziges Buch geschrieben. Es trägt den Titel »Mathematical Quickies« und ist 1967 erschienen. Aus diesem Buch stammt das heutige Rätsel.

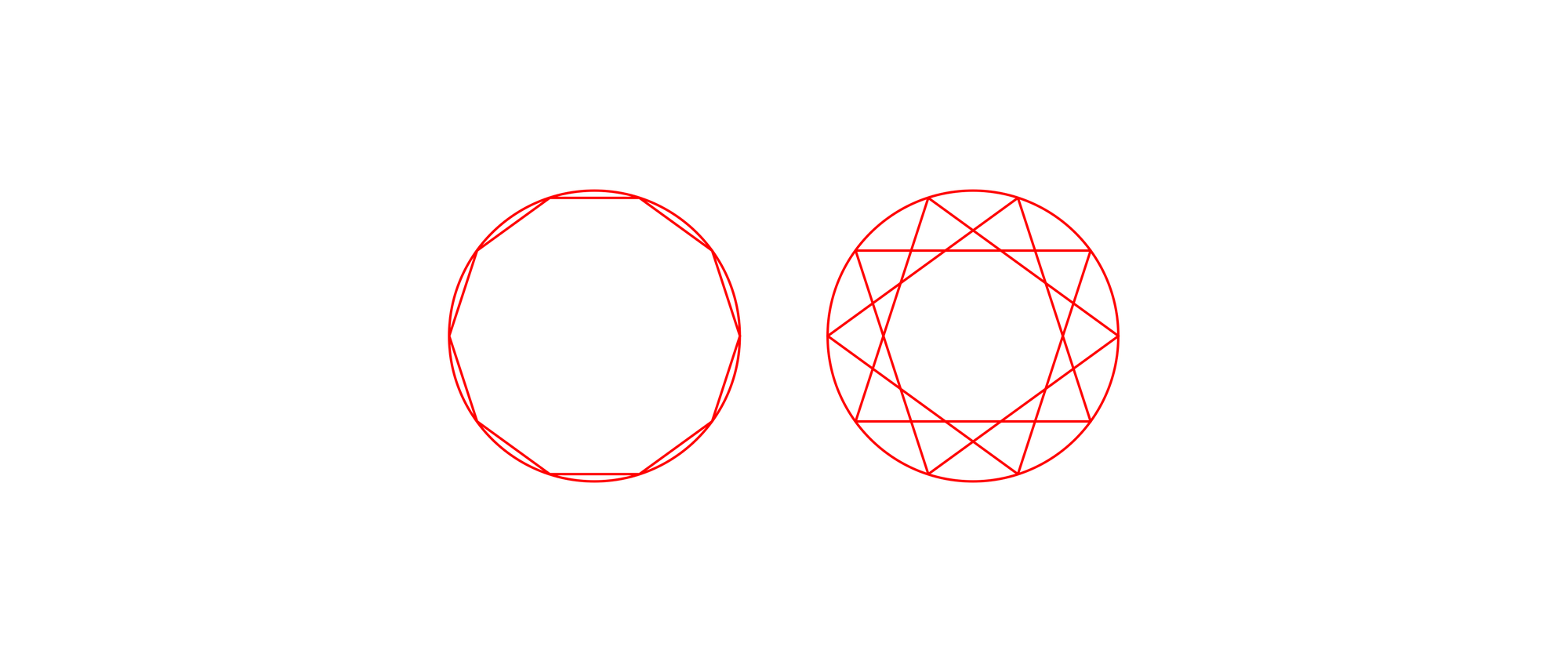
Unterteilt man den Umfang eines Kreises in zehn gleiche Stücke und verbindet alle benachbarten Teilungspunkte miteinander, erhält man ein regelmäßiges Zehneck. Verbindet man jedoch nicht die benachbarten Teilungspunkte, sondern die jeweils überübernächsten Nachbarn, so entsteht ein Sternzehneck. Angenommen, der Kreis hat einen Radius von zehn Zentimetern, wie groß ist dann die Differenz zwischen der Seitenlänge des Sternzehnecks und der des regelmäßigen Zehnecks? Eine Seite des Sternzehnecks ist dabei eine komplette Kreissehne und nicht nur die Kante einer Zacke.