Hemmes mathematische Rätsel: Das zerschnittene Oktaeder
Der griechische Philosoph Platon beschrieb in seinen Werken die fünf regelmäßigen konvexen Polyeder, die man deshalb heute auch als die Platonischen Körper bezeichnet. Eines davon ist das reguläre Oktaeder. Es wird von acht gleichen gleichseitigen Dreiecken begrenzt. Alle Seitenflächen schließen mit ihren Nachbarn den gleichen Winkel ein. Man nennt das Oktaeder oft auch reguläre quadratische Doppelpyramide, weil man es sich aus zwei Pyramiden zusammengesetzt vorstellen kann, die mit ihren Grundflächen aufeinander stehen. Im April 1965 stellte der amerikanische Mathematiker und Ingenieur Charles Wilderman Trigg (1898–1989) in der Zeitschrift »Mathematics Magazine« dazu folgende Aufgabe:
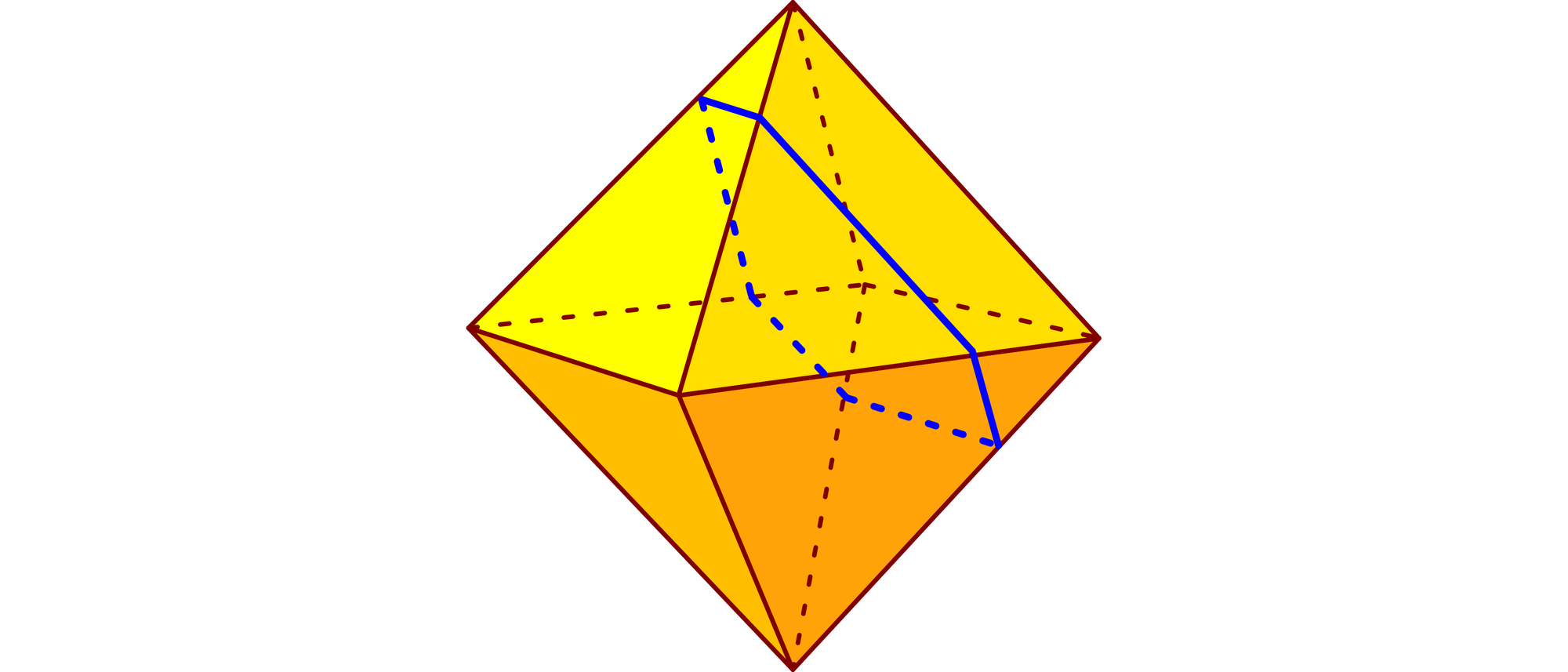
Ein reguläres Oktaeder mit einer Seitenlänge von zehn Zentimetern wird parallel und im Abstand von drei Zentimetern zu einer seiner Seitenflächen durchgeschnitten. Wie groß ist der Umfang der Schnittfläche?
Ein Oktaedernetz besteht aus acht zusammenhängenden gleichseitigen Dreiecken. Man kann es auf Karton zeichnen, ausschneiden, knicken und zu einem regulären Oktaeder zusammenkleben.
Die Lösung der Aufgabe sieht man sofort, wenn man die Schnittlinie in ein Netz des Oktaeders einzeichnet. Sechs der acht Dreiecke bilden ein Parallelogramm, und die Schnittlinie verläuft parallel zu seinen beiden langen Seiten. Sie hat, unabhängig in welchem Abstand zu den langen Parallelogrammseiten der Schnitt erfolgt, immer einen Umfang von drei Dreieckseitenlängen oder 30 Zentimetern.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.