Hemmes mathematische Rätsel: Die Ameisen auf dem Würfel
Martin Gardner wurde 1914 in Tulsa in Oklahoma geboren und schrieb über ein Vierteljahrhundert lang für das amerikanische Wissenschaftsmagazin »Scientific American« die Kolumne »Mathematical Games«, in der er unterhaltsam über die Mathematik berichtete, mathematische Spielereien und Knobeleien vorstellte und den Lesern Rätsel zu lösen gab. Gardner wurde weltbekannt, und Monat für Monat lasen Hunderttausende begeistert seine Kolumne. Gardners Artikel wurden zu mehr als einem Dutzend Bücher zusammengefasst und in vielen Sprachen zu Bestsellern. Am 22. Mai 2010 starb Martin Gardner im Alter von 95 Jahren. Im Juni 1969 veröffentlichte er folgendes Rätsel:
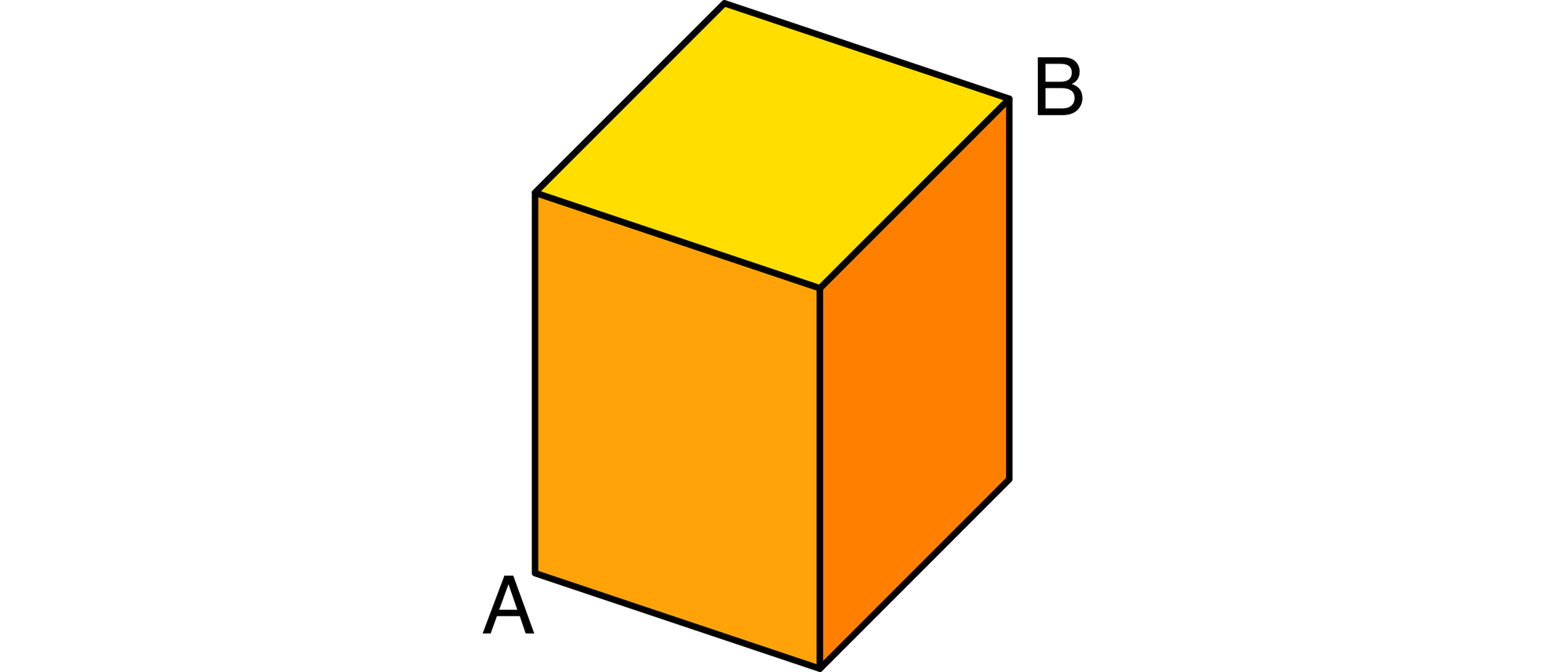
Eine Kolonne Ameisen trifft auf die Ecke A eines Würfels. Die Ameisen beginnen nun entlang der Kanten über den Würfel zu krabbeln. Alle Ameisen entscheiden an jeder Ecke des Würfels per Zufall, entlang welcher Kante sie von da aus weiterkrabbeln. Jede der drei Kanten, die an einer Ecke zusammenstoßen, kann dabei mit der gleichen Wahrscheinlichkeit gewählt werden, also auch die, über die die Ameisen zu dieser Ecke gelangt sind. An der Ecke B des Würfels klebt ein Tropfen Honig. Sobald eine Ameise diese Ecke erreicht hat, beendet sie ihre Wanderung über den Würfel. Wie viele Kanten weit muss eine Ameise im Mittel krabbeln, um von der Ecke A zur Ecke B zu gelangen?
Wir nennen die drei über eine Kante direkt mit der Ecke A verbundenen Ecken X und die direkt mit B verbundenen Ecken Y. Wegen der Symmetrie brauchen die drei Ecken X und die drei Ecken Y nicht weiter unterschieden zu werden.
Mit nE bezeichnen wir die zu erwartende Anzahl von Kanten, die eine Ameise von einer Ecke E bis zum Ziel B noch zurücklegt. Von der Startecke A aus gelangt eine Ameise, wenn sie eine Kante weit krabbelt, immer zu einer Ecke X. Das heißt, nA = nX + 1. Von einer Ecke X aus erreicht eine Ameise über die nächste Kante in zwei von drei Fällen eine Ecke Y und im dritten Fall die Ecke A. Es gilt also nX = 2⁄3nY + 1⁄3nA + 1. Von der Ecke Y aus gelangt eine Ameise über die nächste Kante in zwei von drei Fällen zur Ecke X und im dritten Fall zum Ziel B. Folglich ist nY = 2⁄3nX + 1. Setzt man diese drei Gleichungen ineinander ein und löst sie nach nA auf, erhält man nA = 10. Eine Ameise muss also im Mittel zehn Kanten weit krabbeln, um von der Ecke A zur Ecke B zu gelangen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.